题目内容
1．下面的计算正确的是（ ）| A． | 3a-2a=1 | B． | a+2a2=3a3 | C． | -（a-b）=-a+b | D． | 2（a+b）=2a+b |
分析 依据合并同类项法则和去括号法则判断即可．
解答 解：A、3a-2a=a，故A错误；
B、不是同类项不能合并，故B错误；
C、-（a-b）=-a+b，故C正确；
D、2（a+b）=2a+2b，故D错误．
故选：C．
点评 本题主要考查的是合并同类项法则和去括号，掌握合并同类项法则和去括号法则是解题的关键．
练习册系列答案
相关题目
11．已知抛物线y=$\frac{1}{2}$x2-x，它与x轴的两个交点间的距离为（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 4 |
9．
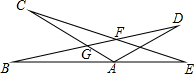如图，点A在BE上，且AC=AB，BD=CE．CE，BD交于点F，AC，BD交于点G．∠CAB=∠DFE．则AE等于（ ）
如图，点A在BE上，且AC=AB，BD=CE．CE，BD交于点F，AC，BD交于点G．∠CAB=∠DFE．则AE等于（ ）| A． | AD | B． | DF | C． | CE-AB | D． | BD-AB |
如图，点A，B，C在直线l上，则图中共有3条线段，有6条射线．
7．为了探究n条直线能把平面最多分成几部分，我们从最简单的情形入手：
（1）一条直线把平面分成2部分；
（2）两条直线最多可把平面分成4部分；
（3）三条直线最多可把平面分成7部分…；
把上述探究的结果进行整理，列表分析：
（1）当直线条数为5时，把平面最多分成16部分，写成和的形式1+1+2+3+4+5；
（2）当直线为n条时，把平面最多分成$\frac{{n}^{2}+n+2}{2}$部分．
（1）一条直线把平面分成2部分；
（2）两条直线最多可把平面分成4部分；
（3）三条直线最多可把平面分成7部分…；
把上述探究的结果进行整理，列表分析：
| 直线条数 | 把平面分成部分数 | 写成和形式 |
| 1 | 2 | 1+1 |
| 2 | 4 | 1+1+2 |
| 3 | 7 | 1+1+2+3 |
| 4 | 11 | 1+1+2+3+4 |
| … | … | … |
（2）当直线为n条时，把平面最多分成$\frac{{n}^{2}+n+2}{2}$部分．