题目内容
7.为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手:(1)一条直线把平面分成2部分;
(2)两条直线最多可把平面分成4部分;
(3)三条直线最多可把平面分成7部分…;
把上述探究的结果进行整理,列表分析:
| 直线条数 | 把平面分成部分数 | 写成和形式 |
| 1 | 2 | 1+1 |
| 2 | 4 | 1+1+2 |
| 3 | 7 | 1+1+2+3 |
| 4 | 11 | 1+1+2+3+4 |
| … | … | … |
(2)当直线为n条时,把平面最多分成$\frac{{n}^{2}+n+2}{2}$部分.
分析 (1)根据已知探究的结果可以算出当直线条数为5时,把平面最多分成16部分;
(2)通过已知探究结果,写出一般规律,当直线为n条时,把平面最多分成1+1+2+3+…+n,求和即可.
解答 解:(1)根据已知探究的结果知:
当直线条数为5时,把平面最多分成1+1+2+3+4+5=16部分,
故答案为:16,1+1+2+3+4+5.
(2))通过已知探究结果,
当直线为n条时,
把平面最多分成:1+1+2+3+3+…+n=$\frac{(1+n)n}{2}$+1=$\frac{{n}^{2}+n+2}{2}$.
故答案为:$\frac{{n}^{2}+n+2}{2}$.
点评 题目考查了图形的变化,通过直线分平面探究其中的隐含规律,解决此题关键是写出和的形式,另外,等差数列求和公式应该应用熟练.

练习册系列答案
相关题目
1.下面的计算正确的是( )
| A. | 3a-2a=1 | B. | a+2a2=3a3 | C. | -(a-b)=-a+b | D. | 2(a+b)=2a+b |
2.已知30m3的物体重900kg,则物体重量P(kg)和体积V(m3)之间的函数关系式为( )
| A. | V=30P | B. | P=V+900 | C. | P=30V | D. | PV=30 |
2.以下列各组数为三角形的边长,能构成直角三角形的是( )
| A. | 8,12,17 | B. | 1,2,3 | C. | 6,8,10 | D. | 5,12,9 |
16.下列各式中正确的是( )
| A. | $\sqrt{16}$=±4 | B. | $\sqrt{{{(-5)}^2}}$=-5 | C. | ±$\sqrt{64}$=±8 | D. | $\root{3}{-27}$=-9 |
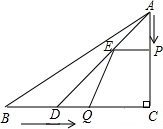 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1厘米/秒的速度沿AC向终点C运动;点Q以1.25厘米/秒的速度沿BC向终点C运动.过点P作PE∥BC交AD于点E,连接EQ.设动点运动时间为t秒(t>0).当一个点到达终点时,另一个点随之停止运动.
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1厘米/秒的速度沿AC向终点C运动;点Q以1.25厘米/秒的速度沿BC向终点C运动.过点P作PE∥BC交AD于点E,连接EQ.设动点运动时间为t秒(t>0).当一个点到达终点时,另一个点随之停止运动.