题目内容
10.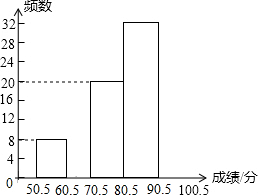 某中学组织了一次“中华民族的伟大复兴”历史知识竞赛,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频率分布直方图如下:
某中学组织了一次“中华民族的伟大复兴”历史知识竞赛,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频率分布直方图如下:| 分组 | 频数 | 频率 |
| 50.5-60.5 | 8 | 0.08 |
| 60.5-70.5 | 12 | 0.12 |
| 70.5-80.5 | 20 | 0.2 |
| 80.5-90.5 | 32 | 0.32 |
| 90.5-100.5 | 28 | a |
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
分析 (1)根据频数=总数×百分数,求出第二组人数,再求出最后一组人数,即可解决问题.
(2)利用样本估计总体的思想解决问题.
解答 解:(1)第一组的频数为8,频率为0.08,
所以被抽取的学生总数为8÷0.08=100(人).
第二组60.5~70.5的频数=100×0.12=12(人).
第三组的频率=$\frac{20}{100}$=0.2,
第四组的频数=100-8-12-20-32=28(人),
第四组是频率=$\frac{32}{100}$=0.32.
故答案分别为8,12,0.2,0.32,28.
所以a=28÷100=0.28.
补全频数分布直方图如下,
(2)1000×$\frac{32+28}{100}$=600(人).
所以这次参赛的学生中成绩为优秀的约为600人.
点评 本题考查频数分布表、用样本估计总体、频数分布表、中位数等知识,解题的关键是记住知识,学会利用样本估计总体的思想解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.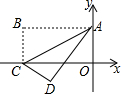 如图,已知矩形纸片OABC在平面直角坐标系中,将该纸片沿对角线AC进行折叠,使得点B到达点D的位置,若该纸片的长为4、宽为2,则点D的坐标为( )
如图,已知矩形纸片OABC在平面直角坐标系中,将该纸片沿对角线AC进行折叠,使得点B到达点D的位置,若该纸片的长为4、宽为2,则点D的坐标为( )
 如图,已知矩形纸片OABC在平面直角坐标系中,将该纸片沿对角线AC进行折叠,使得点B到达点D的位置,若该纸片的长为4、宽为2,则点D的坐标为( )
如图,已知矩形纸片OABC在平面直角坐标系中,将该纸片沿对角线AC进行折叠,使得点B到达点D的位置,若该纸片的长为4、宽为2,则点D的坐标为( )| A. | (-$\frac{12}{5}$,-$\frac{6}{5}$) | B. | (-$\frac{12}{5}$,-$\frac{8}{5}$) | C. | ($\frac{12}{5}$,-$\frac{6}{5}$) | D. | ($\frac{12}{5}$,-$\frac{8}{5}$) |
 如图,AD为△ABC的中线,E是AD的中点,若△ABC的面积为40,BD=5,则△BDE中BD边上的高为4.
如图,AD为△ABC的中线,E是AD的中点,若△ABC的面积为40,BD=5,则△BDE中BD边上的高为4. 如图,已知BC∥DE,∠ABC=120°,那么直线AB、DE的夹角是120°或60°.
如图,已知BC∥DE,∠ABC=120°,那么直线AB、DE的夹角是120°或60°.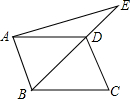 如图,点E在平行四边形ABCD的对角线BD的延长线上.
如图,点E在平行四边形ABCD的对角线BD的延长线上.