题目内容
18. 如图,P为正方形ABCD内一点,且PC=3,∠APB=135°,将△APB绕点B顺时针旋转90°得到△CP′B,连接PP′.若BP的长为整数,则AP=$\sqrt{7}$或1.
如图,P为正方形ABCD内一点,且PC=3,∠APB=135°,将△APB绕点B顺时针旋转90°得到△CP′B,连接PP′.若BP的长为整数,则AP=$\sqrt{7}$或1.
分析 根据旋转性质可得∠APB=∠CP'B=135°、∠ABP=∠CBP'、BP=BP'、AP=CP',由∠ABP+∠PBC=90°知△BPP'是等腰直角三角形,进而根据∠CP'B=135°可得∠PP'C=90°,设BP=BP'=a、AP=CP'=b,在RT△PP'C中根据勾股定理可得CP'=$\sqrt{9-2{a}^{2}}$,最后由BP的长a为整数可得AP.
解答 解:∵△BP'C是由△BPA旋转得到,
∴∠APB=∠CP'B=135°,∠ABP=∠CBP',BP=BP',AP=CP',
∵∠ABP+∠PBC=90°,
∴∠CBP'+∠PBC=90°,即∠PBP'=90°,
∴△BPP'是等腰直角三角形,
∴∠BP'P=45°,
∵∠APB=∠CP'B=135°,
∴∠PP'C=90°,
设BP=BP'=a,AP=CP'=b,
则PP'=$\sqrt{2}$a,
在RT△PP'C中,∵PP'2+P'C2=PC2,且PC=3,
∴CP'=$\sqrt{P{C}^{2}-PP{'}^{2}}$=$\sqrt{9-2{a}^{2}}$,
∵BP的长a为整数,
∴满足上式的a为1或2,
当a=1时,AP=CP'=$\sqrt{7}$,
当a=2时,AP=CP'=1,
故答案为:$\sqrt{7}$或1.
点评 本题主要考查旋转的性质、等腰直角三角形、勾股定理等知识点,熟练运用这些性质、定理得出a、b间的关系式是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.若关于x的一元二次方程(x-2)(x-3)=m有实数根x1、x2,且x1<x2,则下列结论中错误的是( )
| A. | 当m=0时,x1=2,x2=3 | |
| B. | m>-$\frac{1}{4}$ | |
| C. | 当m>0时,2<x1<x2<3 | |
| D. | 二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0) |
7.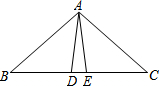 如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )
如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )
 如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )
如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )| A. | △ABE≌△ACD | B. | △ABD≌△ACE | C. | ∠C=30° | D. | ∠DAE=40° |
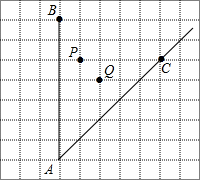 如图,在边长为1个单位长度的小正方形组成的网格中,请分别在边AB,AC上找到点E,F,使四边形PEFQ的周长最小.
如图,在边长为1个单位长度的小正方形组成的网格中,请分别在边AB,AC上找到点E,F,使四边形PEFQ的周长最小.