题目内容
14.已知四张卡片上面分别写着6,x+1,x2-1,x-1,从中任意选两个整式.其中能组成最简分式的有$\frac{6}{x+1}$,$\frac{6}{{x}^{2}-1}$,$\frac{6}{x-1}$,$\frac{x+1}{x-1}$,$\frac{x-1}{x+1}$.分析 根据最简分式的定义写出最简分式即可.
解答 解:能组成最简分式的有$\frac{6}{x+1}$,$\frac{6}{{x}^{2}-1}$,$\frac{6}{x-1}$,$\frac{x+1}{x-1}$,$\frac{x-1}{x+1}$;
故答案为:$\frac{6}{x+1}$,$\frac{6}{{x}^{2}-1}$,$\frac{6}{x-1}$,$\frac{x+1}{x-1}$,$\frac{x-1}{x+1}$.
点评 此题考查了最简分式,最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
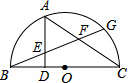 如图,BC是半圆O的直径,点G是半圆上任意一点,点A为BG的中点,AD⊥BC于E,AC与BG交于点F.
如图,BC是半圆O的直径,点G是半圆上任意一点,点A为BG的中点,AD⊥BC于E,AC与BG交于点F.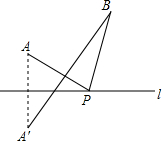 如图,点A′与点A关于直线l对称,点B与点A在直线l的同侧,连接A′B,测得A′B=10cm.若点P为直线l上的一个动点,连接PA,PB,则PA+PB的最小值为10cm.
如图,点A′与点A关于直线l对称,点B与点A在直线l的同侧,连接A′B,测得A′B=10cm.若点P为直线l上的一个动点,连接PA,PB,则PA+PB的最小值为10cm.