题目内容
已知x2-y2-z2=0,A是关于x,y,z的一次的多项式,且x3-y3-z3=(x-y)(x-z)A,则A的表达式是 .
考点:整式的混合运算
专题:计算题
分析:由积除以一个因式得到另一个因式表示出A,记作①,由已知等式变形得到x2=y2+z2②;y2=x2-z2③;z2=x2-y2④,由②表示出x3,代入A中计算即可得到结果.
解答:解:由题意得:A=
①,
由x2-y2-z2=0,得到x2=y2+z2②;y2=x2-z2③;z2=x2-y2④,
由②变形得:x3=xy2+xz2,
则A=
=
+
⑤,
把③④代入⑤化简得:A=2x+y+z.
故答案为:A=2x+y+z.
| x3-y3-z3 |
| (x-y)(x-z) |
由x2-y2-z2=0,得到x2=y2+z2②;y2=x2-z2③;z2=x2-y2④,
由②变形得:x3=xy2+xz2,
则A=
| xy2+xz2-y3-z3 |
| (x-y)(x-z) |
| y2 |
| x-z |
| z2 |
| x-y |
把③④代入⑤化简得:A=2x+y+z.
故答案为:A=2x+y+z.
点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
 如图,直线AB与y轴、x轴交点分别为A(0,2)、B(4,0),求直线AB的解析式及△AOB的面积.
如图,直线AB与y轴、x轴交点分别为A(0,2)、B(4,0),求直线AB的解析式及△AOB的面积.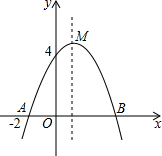 已知二次函数y=ax2+bx+c的图象如图的所示.
已知二次函数y=ax2+bx+c的图象如图的所示. 如图,P是⊙O外一点,PA、PB分别和⊙O切于A、B两点,PA=4cm,∠P=40°,C是AB上任意一点,过点C作⊙O的切线,分别交PA、PB于点D、E,求:
如图,P是⊙O外一点,PA、PB分别和⊙O切于A、B两点,PA=4cm,∠P=40°,C是AB上任意一点,过点C作⊙O的切线,分别交PA、PB于点D、E,求: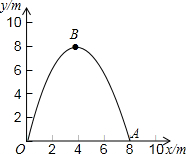 如图,某人从原点O处打网球,网球的飞行路线是抛物线,可用二次函数y=4x-
如图,某人从原点O处打网球,网球的飞行路线是抛物线,可用二次函数y=4x-