题目内容
3. 如图,四边形ABCD与ECGF是两个边长分别为a,b的正方形,
如图,四边形ABCD与ECGF是两个边长分别为a,b的正方形,(1)用a,b表示△BGF的面积的代数式S1=$\frac{1}{2}$b2+$\frac{1}{2}$ab;
(2)求出阴影部分的面积的代数式S2(用a,b表示)
(3)当a=4cm,b=6cm时,阴影部分的面积.
分析 (1)求出BG、FG的长度即可求出△BGF的长度.
(2)设BF与CD交于点D,易证△BCH∽△BGF,利用相似三角形的性质求出CH的长度,进而求出EH的长度,最后即可求出S2的代数式.
(3)将a与b的值代入(2)中的代数式即可求出答案.
解答 解:(1)∵BG=BC+CG=a+b,FG=b,
∴S1=$\frac{1}{2}$FG•BG=$\frac{1}{2}$b(a+b)=$\frac{1}{2}$b2+$\frac{1}{2}$ab
(2) ∵CH∥FG,
∵CH∥FG,
∴△BCH∽△BGF,
∴$\frac{BC}{BG}=\frac{CH}{GF}$,
∴CH=$\frac{ab}{a+b}$,
∴DH=a-$\frac{ab}{a+b}$=$\frac{{a}^{2}}{a+b}$,
EH=b-$\frac{ab}{a+b}$=$\frac{{b}^{2}}{a+b}$,
∴S2=S△BDH+S△HEF
=$\frac{1}{2}$DH•BC+$\frac{1}{2}$EH•EF
=$\frac{1}{2}$×$\frac{{a}^{2}}{a+b}$×a+$\frac{1}{2}$×$\frac{{b}^{2}}{a+b}$×b
=$\frac{{a}^{3}+{b}^{3}}{2(a+b)}$
=$\frac{(a+b)({a}^{2}-ab+{b}^{2})}{2(a+b)}$
=$\frac{{a}^{2}-ab+{b}^{2}}{2}$
(3)当a=4,b=6时,
S2=$\frac{16-24+36}{2}$=14cm2
故答案为:(1)$\frac{1}{2}$b2+$\frac{1}{2}$ab
点评 本题考查代数式求值,涉及相似三角形的性质与判定,因式分解,有理数混合运算等知识,综合程度较高.

 如图,AC=DF,AC∥DF,AE=DB.
如图,AC=DF,AC∥DF,AE=DB.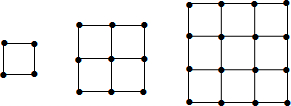

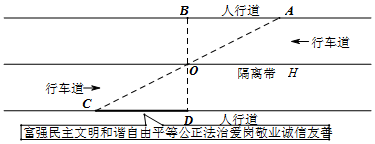
 如图所示,四边形OABC是矩形,点D在OC边上,以AD为折痕,将△OAD向上翻折,点O恰好落在BC边上的点E处,若△ECD的周长为4,△EBA的周长为12.
如图所示,四边形OABC是矩形,点D在OC边上,以AD为折痕,将△OAD向上翻折,点O恰好落在BC边上的点E处,若△ECD的周长为4,△EBA的周长为12. 如图,由18个棱长为a厘米的正方形拼成的立体图形,它的表面积是48a2cm2.
如图,由18个棱长为a厘米的正方形拼成的立体图形,它的表面积是48a2cm2.