题目内容
11.x2-x-1=0 根是x1=$\frac{1+\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$.,m2-4m+5的最小值是1.分析 利用求根公式,求出一元二次方程x2-x-1=0的根;利用配方的办法把m2-4m+5变形成( )2+正数的形式,再根据非负数的性质确定其最小值.
解答 解:因为x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$
=$\frac{1±\sqrt{1+4}}{2}$
=$\frac{1±\sqrt{5}}{2}$
所以x1=$\frac{1+\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$.
m2-4m+5
=m2-4m+4+1
=(m-2)2+1
因为(m-2)2≥0
所以m2-4m+5的最小值是1
故答案为:x1=$\frac{1+\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$;1.
点评 本题考查了一元二次方程的解法、配方法个非负数的性质.方程ax2+bx+c=0的求根公式为:x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$(2-4ac≥0),初中阶段接触的三种非负数是:$\sqrt{a}$,|a|,a2.

练习册系列答案
相关题目
10.下列各式中运算正确的是( )
| A. | 4y-5y=-1 | B. | 3x2+2x2=5x4 | C. | ab+3ab=4ab | D. | 2a2b-2ab2=0 |
 如图,在四边形ABCD中,AD=BC,AB=CD.
如图,在四边形ABCD中,AD=BC,AB=CD. 已知:如图,AB=DC,AB∥DC,求证:AD=BC.
已知:如图,AB=DC,AB∥DC,求证:AD=BC. 如图,四边形ABCD与ECGF是两个边长分别为a,b的正方形,
如图,四边形ABCD与ECGF是两个边长分别为a,b的正方形,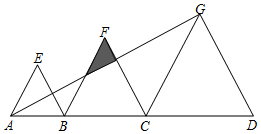 如图,点B、C是线段AD上的点,△ABE、△BCF、△CDG都是等边三角形,且AB=4,BC=6,已知△ABE与△CDG的相似比为2:5.则
如图,点B、C是线段AD上的点,△ABE、△BCF、△CDG都是等边三角形,且AB=4,BC=6,已知△ABE与△CDG的相似比为2:5.则