题目内容
2.先阅读下列材料,再解决问题:阅读材料:数学上有一种根号内又带根号的数,它们能通过完全平方公式及二次根式的性质化去一层根号.
例如:
$\sqrt{3+2\sqrt{2}}$=$\sqrt{3+2×1×\sqrt{2}}$=$\sqrt{{1}^{2}+(\sqrt{2})^{2}+2×1×\sqrt{2}}$=$\sqrt{(1+\sqrt{2})^{2}}$=|1+$\sqrt{2}$|=1+$\sqrt{2}$
解决问题:
①在括号内填上适当的数:
$\sqrt{14+6\sqrt{5}}$=$\sqrt{14+2×3×\sqrt{5}}$=$\sqrt{()^{2}+()^{2}+2×3×\sqrt{5}}$=$\sqrt{()^{2}}$=|3+$\sqrt{5}$|=3+$\sqrt{5}$
②根据上述思路,试将$\sqrt{28-10\sqrt{3}}$予以化简.
分析 ①根据题目中的例子可以解答本题;
②根据题目中的例子可以解答本题.
解答 解:①$\sqrt{14+6\sqrt{5}}$
=$\sqrt{14+2×3×\sqrt{5}}$
=$\sqrt{{3}^{2}+(\sqrt{5})^{2}+2×3×\sqrt{5}}$
=$\sqrt{(3+\sqrt{5})^{2}}$
=|3+$\sqrt{5}$|
=3+$\sqrt{5}$,
故答案为:3+$\sqrt{5}$,3+$\sqrt{5}$;
②$\sqrt{28-10\sqrt{3}}$
=$\sqrt{{5}^{2}+(\sqrt{3})^{2}-2×5×\sqrt{3}}$
=$\sqrt{(5-\sqrt{3})^{2}}$
=|5-$\sqrt{3}$|
=5-$\sqrt{3}$.
点评 本题考查二次根式的性质与化简,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列各式中运算正确的是( )
| A. | 4y-5y=-1 | B. | 3x2+2x2=5x4 | C. | ab+3ab=4ab | D. | 2a2b-2ab2=0 |

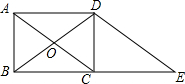 如图,在矩形ABCD中,AB=2,AD=3,对角线AC、BD相交于点O,过点D作DE∥AC交BC延长线于点E.
如图,在矩形ABCD中,AB=2,AD=3,对角线AC、BD相交于点O,过点D作DE∥AC交BC延长线于点E. 如图,四边形ABCD与ECGF是两个边长分别为a,b的正方形,
如图,四边形ABCD与ECGF是两个边长分别为a,b的正方形,