Question

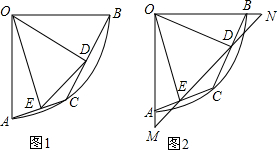
已知EC⊥AD于C，在EC取一点B，使BC=CD，连AB并延长交DE于F，AC=CE．
（1）求证：AB=DE．
（2）求证：FA⊥DE．

Answer 1

考点：全等三角形的判定与性质

专题：证明题

分析：（1）利用SAS证得△ABC≌△EDC，进一步得出结论即可；
（2）利用（1）的△ABC≌△EDC，得出∠E=∠A，结合∠ABC=∠EBF，进一步利用∠A+∠ABC=90°证得结论．

解答：（1）证明：∵EC⊥AD，
∴∠ACE=∠ECD=90°，
在△ABC和△EDC中，

BC=DC ∠ACB=∠ECD AC=CE

，
∴△ABC≌△EDC（SAS），
∴AB=DE．
（2）证明：∵△ABC≌△EDC，
∴∠E=∠A，
又∵∠ABC=∠EBF，∠A+∠ABC=90°，
∴∠E+∠EBF=90°，
即FA⊥DE．

点评：此题考查三角形全等的判定与性质，掌握判定方法是解决问题的关键．