题目内容
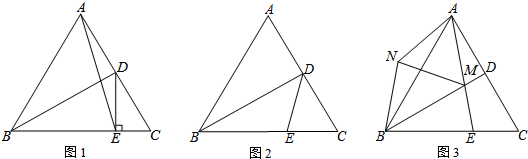
8.如图,等边△ABC的边长为4,BD为AC边上的中线,E为BC边上一点(不与B、C重合).(1)如图1,若DE⊥BC,连接AE,求AE的长;
(2)如图2,若DE平分∠BDC,求BE的长;
(3)如图3,连接AE,交BD于点M.以AM为边作等边△AMN,连接BN.请猜想∠CAE、∠CBD、∠BMN之间的数量关系,并证明你的结论.
分析 (1)如图1,过A作AF⊥于F,由等边△ABC的边长为4,BD为AC边上的中线,得到CD=$\frac{1}{2}$AC=2,∠C=60°,CF=$\frac{1}{2}$AC=2,根据勾股定理即可得到结论;
(2)如图2,过E作EM⊥CD于M,根据等边三角形的性质得到CD=$\frac{1}{2}$AC=2,∠C=60°,BD⊥AC,由角平分线的定义得到∠EDM=45°,然后解直角三角形即可得到结论;
(3)由等边三角形的性质得到∠ADM=90°,由△AMN是等边三角形,得到∠AMN=60°,根据平角的定义得到∠BMN+∠BME=120°,根据对顶角的性质和直角三角形的性质得到∠BME=∠AMD=90°-∠EAC,然后等量代换即可得到结论.
解答  解:(1)如图1,过A作AF⊥于F,
解:(1)如图1,过A作AF⊥于F,
∵等边△ABC的边长为4,BD为AC边上的中线,
∴CD=$\frac{1}{2}$AC=2,∠C=60°,CF=$\frac{1}{2}$AC=2,
∴CE=$\frac{1}{2}$CD=1,AF=2$\sqrt{3}$,
∴EF=1,
∴AE=$\sqrt{A{F}^{2}+E{F}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{1}^{2}}$=$\sqrt{13}$;
(2)如图2,过E作EM⊥CD于M,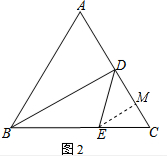
∵等边△ABC的边长为4,BD为AC边上的中线,
∴CD=$\frac{1}{2}$AC=2,∠C=60°,BD⊥AC,
∵DE平分∠BDC,
∴∠EDM=45°,
∴EM=DM,CM=$\frac{\sqrt{3}}{3}$EM=$\frac{\sqrt{3}}{3}$DM,
∴DM+CM=(1+$\frac{\sqrt{3}}{3}$)EM=CD=2,
∴EM=3-$\sqrt{3}$,
∴CE=2$\sqrt{3}$-2,
∴BE=BC-CE=6-2$\sqrt{3}$;
(3)∠CAE+∠CBD=∠BMN,
证明:∵∠ADM=90°,
∵△AMN是等边三角形,
∴∠AMN=60°,
∴∠BMN+∠BME=120°,
∵∠BMN=∠AMD=90°-∠EAC,
∴∠BMN+90°-∠EAC=120°,
∴∠BMN-∠CAE=30°,
∵∠DBC=30°,
∴∠BMN-∠CAE=∠DBC,
即∠CAE+∠CBD=∠BMN.
点评 本题考查了等边三角形的性质,解直角三角形,正确的作出辅助线是解题的关键.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案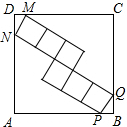 在边长为10的正方形ABCD中,内接有6个大小相同的正方形,P、Q、M、N是落在大正方形边上的小正方形的顶点,如图所示,则这六个小正方形的面积是( )
在边长为10的正方形ABCD中,内接有6个大小相同的正方形,P、Q、M、N是落在大正方形边上的小正方形的顶点,如图所示,则这六个小正方形的面积是( )| A. | $\frac{134}{25}$ | B. | $\frac{408}{25}$ | C. | $\frac{816}{25}$ | D. | $\frac{{12\sqrt{34}}}{5}$ |
| A. | 80° | B. | 40° | C. | 140° | D. | 40°或140° |
 在△ABC中,∠ABC=100°,且∠AEF=∠AFE,∠CFD=∠CDF,那么∠EFD的度数是多少?
在△ABC中,∠ABC=100°,且∠AEF=∠AFE,∠CFD=∠CDF,那么∠EFD的度数是多少?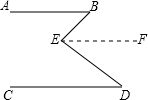 如图,已知∠BED=∠B+∠D,试说明AB与CD的关系.
如图,已知∠BED=∠B+∠D,试说明AB与CD的关系.