题目内容
16.如图(1),已知Rt△ABC的直角边AC的长为2,以AC为直径的⊙O与斜边AB交于点D,过D点作⊙O的切线交BC于点E.(1)求证:BE=DE;
(2)延长DE与AC的延长线交于点F,若DF=$\sqrt{3}$,求△ABC的面积.
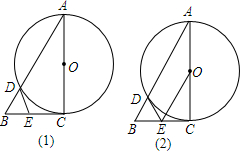
分析 (1)连结OD,如图(1),根据切线的性质得∠ODE=90°,则∠BDE+∠ADO=90°,加上∠ODA=∠A,∠A+∠B=90°,所以∠B=∠BED,于是可判断BE=DE;
(2)如图(2),在Rt△ODF中利用正切定义可计算出∠DOF=60°,则∠A=30°,再在Rt△ABC中利用正切定义计算出BC=$\frac{2\sqrt{3}}{3}$,然后根据三角形面积公式求解.
解答 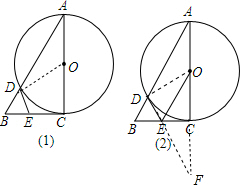 (1)证明:连结OD,如图(1),
(1)证明:连结OD,如图(1),
∵DE为⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,
∴∠BDE+∠ADO=90°,
∵OA=OD,
∴∠ODA=∠A,
而∠A+∠B=90°,
∴∠B=∠BED,
∴BE=DE;
(2)解:如图(2),
在Rt△ODF中,∵OD=1,DF=$\sqrt{3}$,
∴tan∠DOF=$\frac{DF}{OD}$=$\frac{\sqrt{3}}{1}$,
∴∠DOF=60°,
∴∠A=30°,
在Rt△ABC中,∵tanA=$\frac{BC}{AC}$,
∴BC=2tan30°=$\frac{2\sqrt{3}}{3}$,
∴△ABC的面积=$\frac{1}{2}$×2×$\frac{2\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了解直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
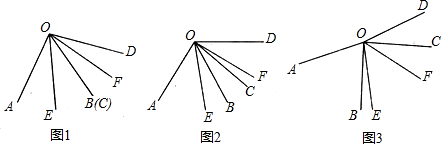
 图1中共有6个三角形,图2中有50个正方形.
图1中共有6个三角形,图2中有50个正方形.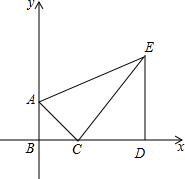 已知,如图,B为坐标原点,A(0,3),D(10,0),E(10,8),点C是线段BD上的动点.
已知,如图,B为坐标原点,A(0,3),D(10,0),E(10,8),点C是线段BD上的动点.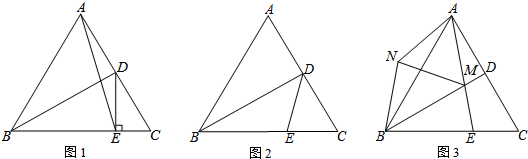
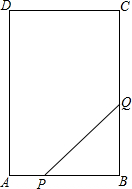 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB边向点B以1cm/s的速度运动,同时,点Q从点B出发沿BC边向点C以2cm/s的速度运动,P,Q两点在分别到达B,C两点后就停止运动,设经过ts时,△PBQ的面积为S cm2
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB边向点B以1cm/s的速度运动,同时,点Q从点B出发沿BC边向点C以2cm/s的速度运动,P,Q两点在分别到达B,C两点后就停止运动,设经过ts时,△PBQ的面积为S cm2