题目内容
18. 在△ABC中,∠ABC=100°,且∠AEF=∠AFE,∠CFD=∠CDF,那么∠EFD的度数是多少?
在△ABC中,∠ABC=100°,且∠AEF=∠AFE,∠CFD=∠CDF,那么∠EFD的度数是多少?
分析 在△ABC中,∠ABC=100°,由三角形的内角和得到∠A+∠C=180°-100°=80°,根据三角形的内角和得到∠AEF+∠AFE+∠A+∠CFD+∠CDF+∠C=360°,于是求得∠AEF+∠AFE+∠CFD+∠CDF=240°,根据已知条件得到∠AFE+∠CFD=$\frac{1}{2}$×240°=120°,于是求得结果.
解答 解:∵在△ABC中,∠ABC=100°,
∴∠A+∠C=180°-100°=80°,
∵∠AEF+∠AFE+∠A+∠CFD+∠CDF+∠C=360°,
∴∠AEF+∠AFE+∠CFD+∠CDF=240°,
∵∠AEF=∠AFE,∠CFD=∠CDF,
∴∠AFE+∠CFD=$\frac{1}{2}$×240°=120°,
∴∠DFE=180°-120°=60°.
点评 本题考查了三角形的内角和,平角的定义,熟练掌握三角形的内角和是解题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
16.开学初,学校食堂领导为了满足需要,去某米商处购买大米,已知每袋大米的标准重量为50千克,30袋大米的称重如下(超出的记为“+”,不足的记为“-”):
(1)与标准重量比较,30袋大米总计超过了多少千克或不足多少千克?
(2)30袋大米的总重量是多少千克?
(3)与标准质量相比不足或者超过1.5千克的包装都是不合格的,请问这30袋大米中有多少袋式包装不合格的?
| -1.6 | -1.2 | -1 | 0 | 1.2 | 1.4 | 1.8 |
| 1 | 5 | 4 | 8 | 6 | 4 | 2 |
(2)30袋大米的总重量是多少千克?
(3)与标准质量相比不足或者超过1.5千克的包装都是不合格的,请问这30袋大米中有多少袋式包装不合格的?
 已知,如图所示,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,∠A=∠BDC=90°,求四边形ABCD的面积.
已知,如图所示,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,∠A=∠BDC=90°,求四边形ABCD的面积.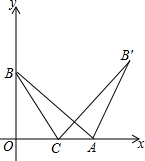 如图,在平面直角坐标系xOy中,点A、B分别在x轴,y轴的正半轴上,且OA=OB,将线段AB绕点A顺时针旋转60°得到AB′,C是x轴上一点,BC+B′C的值最小是B′D,∠OCB=60°.
如图,在平面直角坐标系xOy中,点A、B分别在x轴,y轴的正半轴上,且OA=OB,将线段AB绕点A顺时针旋转60°得到AB′,C是x轴上一点,BC+B′C的值最小是B′D,∠OCB=60°. 已知函数y=mx与y=kx+b的图象经过点A(3,-4),且y=kx+b的图象交y轴于点B,若△OAB是以OA为腰的等腰三角形,其中O为坐标原点
已知函数y=mx与y=kx+b的图象经过点A(3,-4),且y=kx+b的图象交y轴于点B,若△OAB是以OA为腰的等腰三角形,其中O为坐标原点