题目内容
8.已知线段AB=a,CD=b,线段CD在直线AB上运动(A在B的左侧,C在D的左侧),|a-2b|与(6-b)2互为相反数.(1)求a,b的值;
(2)若M,N分别是AC,BD的中点,BC=4,求MN的长;
(3)当CD运动到某一时刻,D点与B点重合,P是线段AB延长线上任意一点,问$\frac{PA+PB}{PC}$的值是否改变?若不变,求出其值;若改变,请说明理由.
分析 (1)依据非负数的性质可知a-2b=0,6-b=0,从而可求得a、b的值;
(2)需要分类讨论:①如图1,当点C在点B的右侧时,根据“M、N分别为线段AC、BD的中点”,先计算出AM、DN的长度,然后计算MN=AD-AM-DN;②如图2,当点C位于点B的左侧时,利用线段间的和差关系求得MN的长度;
(3)先求得AC=BC=6,然后求得PA+PB=2PC,从而可求得答案.
解答 解:(1)∵|a-2b|与(6-b)2互为相反数|,
∴|a-2b|+(6-b)2=0,
∴a-2b=0,6-b=0,
∴b=6,a=12,
(2)∵b=6,a=12,
∴AB=12,CD=6.
如图1所示:
∵M、N分别为线段AC、BD的中点,
∴AM=$\frac{1}{2}$AC=$\frac{1}{2}$(AB+BC)=$\frac{1}{2}×(12+4)$=8,
DN=$\frac{1}{2}$BD=$\frac{1}{2}$(CD+BC)=$\frac{1}{2}×(6+4)$=5,
∴MN=AD-AM-DN=12+4+6-8-5=9;
如图2所示:
∵M、N分别为线段AC、BD的中点,
∴AM=$\frac{1}{2}$AC=$\frac{1}{2}$(AB-BC)=4,
DN=$\frac{1}{2}$BD=$\frac{1}{2}$(CD-BC)=1,
∴MN=AD-AM-DN=12+6-4-4-1=9;
综上所述,MN=9.
(3)如图3所示:
∵AB=12,CD=6,
∴AC=12-6=6.
∴AC=BC.
∴$\frac{PA+PB}{PC}$=$\frac{PC+AC+PC-CB}{PC}$=$\frac{2PC}{PC}$=2.
点评 本题主要考查的是两点间的距离,分类讨论是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
9.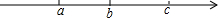 在数轴上表示有理数a,b,c的点如图所示,若ac<0,b+a<0,则( )
在数轴上表示有理数a,b,c的点如图所示,若ac<0,b+a<0,则( )
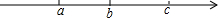 在数轴上表示有理数a,b,c的点如图所示,若ac<0,b+a<0,则( )
在数轴上表示有理数a,b,c的点如图所示,若ac<0,b+a<0,则( )| A. | b+c<0 | B. | |b|<|c| | C. | |a|>|b| | D. | abc<0 |
17.计算($\sqrt{3}$)2-1的结果是( )
| A. | -2 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{3}$-1 |