题目内容
 如图,一次函数y=kx+b的图象与x,y轴交于点A(1,0),B(0,4).
如图,一次函数y=kx+b的图象与x,y轴交于点A(1,0),B(0,4).(1)求该函数的表达式;
(2)若点C,D分别在OA,AB上,且C(0.5,0),D(0.5,m),P为OB上一动点,试求PC+PD的最小值.
考点:轴对称-最短路线问题,待定系数法求一次函数解析式
专题:
分析:(1)根据待定系数法即可求得;
(2)作D点关于y轴的对称点D′,连接CD′交y轴为P点,此时PC+PD=D′C最小;先求得D的坐标,然后求得D的对称点的坐标,根据勾股定理求得D′C,即求得PC+PD的最小值.
(2)作D点关于y轴的对称点D′,连接CD′交y轴为P点,此时PC+PD=D′C最小;先求得D的坐标,然后求得D的对称点的坐标,根据勾股定理求得D′C,即求得PC+PD的最小值.
解答:解:(1)∵一次函数y=kx+b的图象与x,y轴交于点A(1,0),B(0,4),
∴
,
解得
.
∴该函数的表达式为y=-4x+4;
(2)∵点D(0.5,m)在AB上,
∴m=-4×0.5+4=2,
∴D(0.5,2),
作D点关于y轴的对称点D′,连接CD′交y轴为P点,此时PC+PD=D′C最小,
∵D(0.5,2),
∴D′(-0.5,2),
∵C(0,5,0),
∴D′C=
=
,
∴PC+PD的最小值为
.
∴
|
解得
|
∴该函数的表达式为y=-4x+4;
(2)∵点D(0.5,m)在AB上,

∴m=-4×0.5+4=2,
∴D(0.5,2),
作D点关于y轴的对称点D′,连接CD′交y轴为P点,此时PC+PD=D′C最小,
∵D(0.5,2),
∴D′(-0.5,2),
∵C(0,5,0),
∴D′C=
| (0.5+0.5)2+22 |
| 5 |
∴PC+PD的最小值为
| 5 |
点评:本题考查了待定系数法求解析式,轴对称-最短路线问题,根据轴对称求得D′的坐标是关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 青岛农业大学计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1,在温室内,沿左侧内墙保留3米高的空地,其他三侧内墙各保留1米宽的通道,要使蔬菜种植区的面积为288平方米,矩形温室的长与宽各多少米?
青岛农业大学计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1,在温室内,沿左侧内墙保留3米高的空地,其他三侧内墙各保留1米宽的通道,要使蔬菜种植区的面积为288平方米,矩形温室的长与宽各多少米?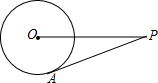 如图,P是⊙O外的一点,PA是⊙O的切线,若PO=13,PA=12,则⊙O的面积和周长分别为( )
如图,P是⊙O外的一点,PA是⊙O的切线,若PO=13,PA=12,则⊙O的面积和周长分别为( )| A、5π,10π |
| B、10π,5π |
| C、25π,10π |
| D、10π,25π |
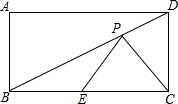 如图,若ABCD是矩形,AB=10cm,BC=20cm,E为边BC上的一个动点,P为BD上的一个动点,求PC+PE的最小值.
如图,若ABCD是矩形,AB=10cm,BC=20cm,E为边BC上的一个动点,P为BD上的一个动点,求PC+PE的最小值. 在平面直角坐标系xOy中,直线y=-
在平面直角坐标系xOy中,直线y=-