题目内容
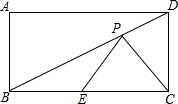 如图,若ABCD是矩形,AB=10cm,BC=20cm,E为边BC上的一个动点,P为BD上的一个动点,求PC+PE的最小值.
如图,若ABCD是矩形,AB=10cm,BC=20cm,E为边BC上的一个动点,P为BD上的一个动点,求PC+PE的最小值.考点:轴对称-最短路线问题
专题:
分析:根据轴对称求最短路线的方法得出P点位置,进而利用三角形相似对应边成比例求出C′E,即可求得PC+PE的值.
解答: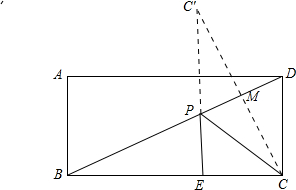 解:如图所示:由题意可得出:作C点关于BD对称点C′,连接BC′,
解:如图所示:由题意可得出:作C点关于BD对称点C′,连接BC′,
过点C′作C′E⊥BC于点E,交BD于点P,连接PC,此时PC+PE=C′E最小,
∵AB=CD=10cm,BC=20cm,
∴BD=
=10
cm,
∵CC′⊥BD,
∴∠BMC=∠BCD=90°,
∴∠BCM=∠BDC,
∴△BCM∽△BDC,
∴
=
,
∴CM=
=
=4
,
∴CC′=8
cm,
∵C′E⊥BC,
∴∠C′EC=∠BCD=90°,
∴△C′EC∽△BCD,
∴
=
,
∴C′E=
=
=16cm;
∴PC+PE的最小值为16cm.
 解:如图所示:由题意可得出:作C点关于BD对称点C′,连接BC′,
解:如图所示:由题意可得出:作C点关于BD对称点C′,连接BC′,过点C′作C′E⊥BC于点E,交BD于点P,连接PC,此时PC+PE=C′E最小,
∵AB=CD=10cm,BC=20cm,
∴BD=
| BC2+DC2 |
| 5 |
∵CC′⊥BD,
∴∠BMC=∠BCD=90°,
∴∠BCM=∠BDC,
∴△BCM∽△BDC,
∴
| CM |
| BC |
| DC |
| BD |
∴CM=
| BC•DC |
| BD |
| 20×10 | ||
10
|
| 5 |
∴CC′=8
| 5 |
∵C′E⊥BC,
∴∠C′EC=∠BCD=90°,
∴△C′EC∽△BCD,
∴
| C′E |
| BC |
| C′C |
| BD |
∴C′E=
| C′C•BC |
| BD |
8
| ||
10
|
∴PC+PE的最小值为16cm.
点评:此题主要考查了利用轴对称求最短路线以及三角形相似的判定和性质,利用轴对称得出P点位置是解题关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
下列各式是二次根式的是( )
A、
| |||
B、
| |||
C、
| |||
D、
|
 如图,一次函数y=kx+b的图象与x,y轴交于点A(1,0),B(0,4).
如图,一次函数y=kx+b的图象与x,y轴交于点A(1,0),B(0,4).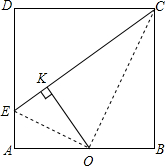 如图,在正方形ABCD的一边上取一点E,使AE=
如图,在正方形ABCD的一边上取一点E,使AE=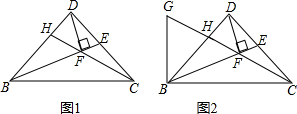
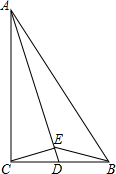 如图,在Rt△ABC中,∠ACB=90°,D是BC中点,CE⊥AD,垂足为E,试判断∠BED与∠ABC是否相等.
如图,在Rt△ABC中,∠ACB=90°,D是BC中点,CE⊥AD,垂足为E,试判断∠BED与∠ABC是否相等.