题目内容
青岛农业大学计划建造如图所示的矩形蔬菜温室，要求长与宽的比为2：1，在温室内，沿左侧内墙保留3米高的空地，其他三侧内墙各保留1米宽的通道，要使蔬菜种植区的面积为288平方米，矩形温室的长与宽各多少米？考点：一元二次方程的应用
专题：几何图形问题
分析：设矩形温室的宽为xm，则长为2xm，根据矩形的面积计算公式即可列出方程求解．
解答：解：设矩形温室的宽为xm，则长为2xm，
根据题意，得（x-2）•（2x-4）=288，
∴2（x-2）2=288，
∴（x-2）2=144，
∴x-2=±12，
解得：x1=-10（不合题意，舍去），x2=14，
所以x=14，2x=2×14=28．
答：当矩形温室的长为28m，宽为14m时，蔬菜种植区域的面积是288m2．
根据题意，得（x-2）•（2x-4）=288，
∴2（x-2）2=288，
∴（x-2）2=144，
∴x-2=±12，
解得：x1=-10（不合题意，舍去），x2=14，
所以x=14，2x=2×14=28．
答：当矩形温室的长为28m，宽为14m时，蔬菜种植区域的面积是288m2．
点评：解答此题，要运用含x的代数式表示蔬菜种植矩形长与宽，再由面积关系列方程．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
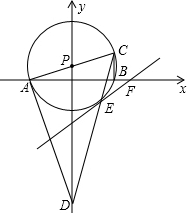如图，已知P（0，1），⊙P与x轴交于A、B两点，AC是⊙P的直径，OA、OD的长是关于x的方程x2-3kx+2k2=0的两根，且OA2+OD2=20．
如图，一次函数y=kx+b的图象与x，y轴交于点A（1，0），B（0，4）．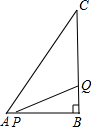
如图，在△ABC中，∠B=90°，AB=6cm，BC=10cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以4cm/s的速度移动．点Q到达点C后，点P、Q停止运动．设P、Q从点A、B同时出发，经过多少秒后，△PBQ的面积是10cm2？