题目内容
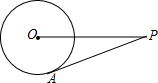 如图,P是⊙O外的一点,PA是⊙O的切线,若PO=13,PA=12,则⊙O的面积和周长分别为( )
如图,P是⊙O外的一点,PA是⊙O的切线,若PO=13,PA=12,则⊙O的面积和周长分别为( )| A、5π,10π |
| B、10π,5π |
| C、25π,10π |
| D、10π,25π |
考点:切线的性质,勾股定理
专题:
分析:连接OA,根据切线的性质证得△AOP是直角三角形,由勾股定理求得OA的长度,然后利用圆的面积、周长公式来求⊙O的面积和周长.
解答: 解:如图,连接OA.
解:如图,连接OA.
∵PA是⊙O的切线,
∴OA⊥AP,即∠OAP=90°.
又∵PO=13,PA=12,
∴根据勾股定理,得
OA=
=
=5,
∴⊙O的面积为:π•OA2=π•52=25π,⊙O的周长为:2π•OA=2π×5=10π.
故选C.
 解:如图,连接OA.
解:如图,连接OA.∵PA是⊙O的切线,
∴OA⊥AP,即∠OAP=90°.
又∵PO=13,PA=12,
∴根据勾股定理,得
OA=
| PO2-PA2 |
| 132-122 |
∴⊙O的面积为:π•OA2=π•52=25π,⊙O的周长为:2π•OA=2π×5=10π.
故选C.
点评:本题考查了切线的性质和勾股定理.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
在△ABC和△A′B′C′中,AB=9cm,BC=8cm,CA=5cm,A′B′=3cm,B′C′=
cm,C′A′=
cm,则( )
| 8 |
| 3 |
| 5 |
| 3 |
| A、∠B=∠A′ |
| B、∠A=∠C′ |
| C、∠A>∠B′ |
| D、∠C=∠B′ |
 如图,一次函数y=kx+b的图象与x,y轴交于点A(1,0),B(0,4).
如图,一次函数y=kx+b的图象与x,y轴交于点A(1,0),B(0,4).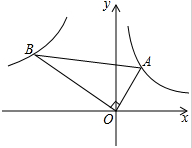 如图,已知第一象限内的点A在反比例函数y=
如图,已知第一象限内的点A在反比例函数y=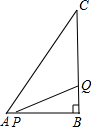 如图,在△ABC中,∠B=90°,AB=6cm,BC=10cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动.点Q到达点C后,点P、Q停止运动.设P、Q从点A、B同时出发,经过多少秒后,△PBQ的面积是10cm2?
如图,在△ABC中,∠B=90°,AB=6cm,BC=10cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动.点Q到达点C后,点P、Q停止运动.设P、Q从点A、B同时出发,经过多少秒后,△PBQ的面积是10cm2?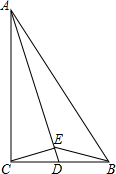 如图,在Rt△ABC中,∠ACB=90°,D是BC中点,CE⊥AD,垂足为E,试判断∠BED与∠ABC是否相等.
如图,在Rt△ABC中,∠ACB=90°,D是BC中点,CE⊥AD,垂足为E,试判断∠BED与∠ABC是否相等.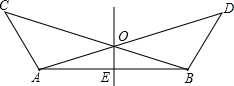 如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.
如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点. 如图所示,⊙O1与⊙O2外切于点P,并且⊙O与⊙O1、⊙O2分别内切于M、N,△O1O2O的周长为36cm,求⊙O的半径长.
如图所示,⊙O1与⊙O2外切于点P,并且⊙O与⊙O1、⊙O2分别内切于M、N,△O1O2O的周长为36cm,求⊙O的半径长.