题目内容
 如图,在边长为l的正方形组成的网络中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1,△AOB关于x轴对称的图形为△A2OB2.
如图,在边长为l的正方形组成的网络中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1,△AOB关于x轴对称的图形为△A2OB2.(1)点B1的坐标为
(2)在旋转过程中,计算点B运动的路径长和线段OB扫过的面积.
考点:作图-旋转变换,弧长的计算,扇形面积的计算
专题:
分析:(1)根据网格结构找出点A1、B1的位置,再与点O顺次连接即可;找出点A2、B2的位置,再与点O顺次连接即可,然后根据平面直角坐标系写出点B1的坐标,确定出点M的位置,再写出点M的坐标;
(2)根据弧长公式和扇形的面积公式分别列式计算即可得解.
(2)根据弧长公式和扇形的面积公式分别列式计算即可得解.
解答: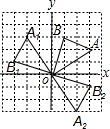 解:(1)B1(-3,1),M(0,0);
解:(1)B1(-3,1),M(0,0);
故答案为:(-1,3),(1,1).
(2)由勾股定理得,OB=
=
,
点B运动的路径长=
=
π,
线段OB扫过的面积=
=
π.
 解:(1)B1(-3,1),M(0,0);
解:(1)B1(-3,1),M(0,0);故答案为:(-1,3),(1,1).
(2)由勾股定理得,OB=
| 12+32 |
| 10 |
点B运动的路径长=
90•π•
| ||
| 180 |
| ||
| 2 |
线段OB扫过的面积=
90•π•(
| ||
| 360 |
| 5 |
| 2 |
点评:本题考查了利用旋转变换作图,利用轴对称变换作图,弧长的计算,扇形的面积的计算,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
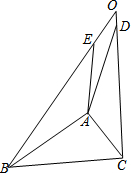 如图,AB、AD是以AB为边向△ABC向外所作正n边形的一组邻边;AC、AE是以AC为边向△ABC外所作正n边形的一组邻边,BE、CD的延长线相交于点O.
如图,AB、AD是以AB为边向△ABC向外所作正n边形的一组邻边;AC、AE是以AC为边向△ABC外所作正n边形的一组邻边,BE、CD的延长线相交于点O. 两个反比例函数
两个反比例函数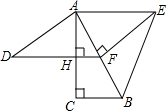 如图,四边形ADFE是平行四边形,EF⊥AF,AH⊥DF,垂足为H,∠FAH=30°,延长AF到点B,使AF=FB,过点B作AH延长线的垂线,垂足为C,连接BE.
如图,四边形ADFE是平行四边形,EF⊥AF,AH⊥DF,垂足为H,∠FAH=30°,延长AF到点B,使AF=FB,过点B作AH延长线的垂线,垂足为C,连接BE. 已知:如图,在矩形ABCD中,AB=10,AD=5,将矩形ABCD折叠,使点C落在边AB上的E处,折痕交DC边于点M,点F在DM上运动,当△AEF是腰长为5的等腰三角形时,EF的长为
已知:如图,在矩形ABCD中,AB=10,AD=5,将矩形ABCD折叠,使点C落在边AB上的E处,折痕交DC边于点M,点F在DM上运动,当△AEF是腰长为5的等腰三角形时,EF的长为 如图,AB∥CD,AE=EF,CE交AB于点F,∠C=110°,则∠A=
如图,AB∥CD,AE=EF,CE交AB于点F,∠C=110°,则∠A= 如图,A,B,C是反比例函数y=
如图,A,B,C是反比例函数y=