题目内容
 两个反比例函数y=
两个反比例函数y=| k1 |
| x |
| k2 |
| x |
| k1 |
| x |
| k2 |
| x |
| k2 |
| x |
考点:反比例函数系数k的几何意义
专题:证明题
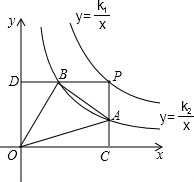
分析:由在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是
|k|,所构成的矩形的面积是|k|,且保持不变,得出S矩形OCPD=k1,S△AOC=S△DBO=
k2,再根据四边形PAOB的面积=S矩形OCPD-S△AOC-S△DBO,化简后即可求出四边形PAOB的面积是k1-k2,为
定值.
| 1 |
| 2 |
| 1 |
| 2 |
定值.
解答:证明:∵动点P在y=
的图象上,PC⊥x轴于点C,交y=
的图象于点A,PD⊥y轴于点D,交y=
的图象于点B,
∴S矩形OCPD=k1,S△AOC=S△DBO=
k2,
∴四边形PAOB的面积=S矩形OCPD-S△AOC-S△DBO=k1-2×
k2=k1-k2.
∴四边形PAOB的面积是定值.
| k1 |
| x |
| k2 |
| x |
| k2 |
| x |
∴S矩形OCPD=k1,S△AOC=S△DBO=
| 1 |
| 2 |
∴四边形PAOB的面积=S矩形OCPD-S△AOC-S△DBO=k1-2×
| 1 |
| 2 |
∴四边形PAOB的面积是定值.
点评:本题考查了反比例函数y=
中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点.
| k |
| x |

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
已知|x|=3,y2=4且x<y,则xy的值等于( )
| A、6 | B、-6 |
| C、6或-6 | D、以上答案都不对 |
 如图,在平面直角坐标系中,已知点A(0,1)、D(-4,4),以AD为边作如图所示的正方形ABCD,顶点在坐标原点的抛物线恰好经过点D,P为抛物线上的一动点.过点E(0,-1)直线L平行于x轴.
如图,在平面直角坐标系中,已知点A(0,1)、D(-4,4),以AD为边作如图所示的正方形ABCD,顶点在坐标原点的抛物线恰好经过点D,P为抛物线上的一动点.过点E(0,-1)直线L平行于x轴.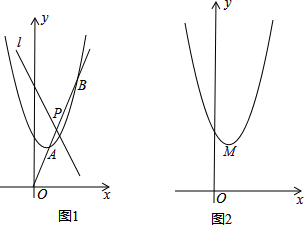
 如图,在边长为l的正方形组成的网络中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1,△AOB关于x轴对称的图形为△A2OB2.
如图,在边长为l的正方形组成的网络中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1,△AOB关于x轴对称的图形为△A2OB2. 边长为2的正方形AOBC如图放置.其中,O为坐标原点.若∠α=15°,则点C的坐标为
边长为2的正方形AOBC如图放置.其中,O为坐标原点.若∠α=15°,则点C的坐标为