Question

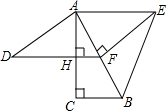如图，四边形ADFE是平行四边形，EF⊥AF，AH⊥DF，垂足为H，∠FAH=30°，延长AF到点B，使AF=FB，过点B作AH延长线的垂线，垂足为C，连接BE．
（1）求证：△ABC≌△EBF； 
（2）已知DH=12，求AB长度．

Answer 1

考点：平行四边形的性质,全等三角形的判定与性质

专题：

分析：（1）利用等边三角形的判定方法得出△AEB是等边三角形，进而得出△ABC≌△EBF（AAS）；
（2）利用锐角三角函数关系得出AH的长，进而得出HF的长，进而得出答案．

解答：（1）证明：∵四边形ADFE是平行四边形，
∴AE=DF，AE∥DF，
∵∠FAH=30°，∠AHF=90°，
∴∠EAF=60°，
∵AF=FB，EF⊥AB，
∴AE=BE，
∴△AEB是等边三角形，
∴AB=BE，∠AEF=∠BEF=30°，
在△ABC和△EBF中，

∠C=∠BFE ∠CAB=∠FEB AB=BE

，
∴△ABC≌△EBF（AAS）；

（2）解：由题意可得出：∠AEF=∠D=30°，
∵DH=12，
∴AH=DHsin30°=12×

3

3

=4

3

，
∴HF=AH×sin30°=4

3

×

3

3

=4，
∴DF=AB=12+4=16．

点评：此题主要考查了全等三角形的判定以及锐角三角函数关系等知识，得出△AEB是等边三角形是解题关键．