Question

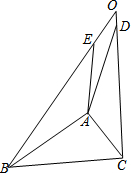如图，AB、AD是以AB为边向△ABC向外所作正n边形的一组邻边；AC、AE是以AC为边向△ABC外所作正n边形的一组邻边，BE、CD的延长线相交于点O．
①猜想：∠BOC的度数为

 

（用含n的式子表示）；
②证明你的猜想．

Answer 1

考点：全等三角形的判定与性质,多边形内角与外角

专题：

分析：①分别以AB、AC为边，向△ABC外作正三角形，正四边形，正五边形，BE、CD相交于点O…得出对应的∠BOC的度数分别为

360

3

，

360

4

，

360

5

…，进一步类推得出∠BOC的度数为

360

n

；
②证明△DAC≌△BAE，根据三角形外角与内角之间的关系就可以求出∠BOC的值，依此类推就可以得出当作n边形的时候就可以求出∠BOC的值．

解答：解：①∠BOC的度数为

360

n

；
②证明：根据题意，得∠BAD和∠CAE都是正n边形的内角，
∵AB=AD，AE=AC．
∴∠BAD=∠CAE=

(n-2)•180°

n

，
∴∠BAD-∠DAE=∠CAE-∠DAE，
即∠BAE=∠DAC，
在△ABE≌△ADC中，

BA=DA ∠BAE=∠DAC AE=AC

∴△ABE≌△ADC（SAS）
∴∠ABE=∠ADC．
则∠ADC+∠ODA=∠ABO+∠ODA=180°，
∵∠ABO+∠ODA+∠DAB+∠BOC=360°，
∴∠DAB+∠BOC=180°，
∴∠BOC=180°-∠DAB=180°-

(n-2)•180°

n

=

360°

n

．

点评：本题考查了正n边形的性质的运用，全等三角形的判定及性质的运用，解答时根据正多边形的性质证明三角形全等是关键．