题目内容
3.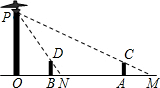 如图,路灯(P点)距地面8米,身高1.6米的小明从距离路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点(B点在A点的左边)时,身影的长度是变长了还是变短了?变长或变短了多少米?
如图,路灯(P点)距地面8米,身高1.6米的小明从距离路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点(B点在A点的左边)时,身影的长度是变长了还是变短了?变长或变短了多少米?
分析 由题意得出△MAC∽△MOP,△NBD∽△NOP,即可由相似三角形的性质求解.
解答 解:∵∠MAC=∠MOP=90°,
∠AMC=∠OMP,
∴△MAC∽△MOP.
∴$\frac{MA}{MO}$=$\frac{AC}{OP}$,
即$\frac{MA}{20+MA}$=$\frac{1.6}{8}$,
解得,MA=5米;
同理,由△NBD∽△NOP,可求得NB=1.5米,
∴小明的身影变短了,变短了5-1.5=3.5(米).
点评 本题考查了相似三角形的应用;解题时关键是找出相似的三角形,根据对应边成比例列出方程.

练习册系列答案
相关题目
11.已知函数y=3(x-2)2+1图象上有三点A(1,y1)、B(4,y2)、C($\sqrt{2}$,y3),试确定y1、y2、y3的大小( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y2<y1 | D. | y3<y1<y2 |
18.小亮在用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出了下面的表格:
由于粗心,他算错了其中一个y值,则这个错误的y值是-2.
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | -2 | -3 | -4 | -3 | 0 | … |
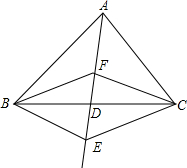 如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE,连结BF,CE.
如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE,连结BF,CE.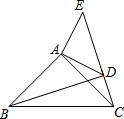 如图,△ACB和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点C、D、E三点在同一直线上,连结BD.求证:
如图,△ACB和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点C、D、E三点在同一直线上,连结BD.求证: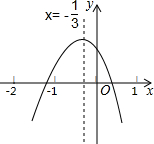 小明从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察到下面四条信息:①ab>0;②a+b+c<0;③b+2c>0;④a=$\frac{3}{2}$b.你认为其中正确信息的个数有( )
小明从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察到下面四条信息:①ab>0;②a+b+c<0;③b+2c>0;④a=$\frac{3}{2}$b.你认为其中正确信息的个数有( )