题目内容
14.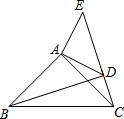 如图,△ACB和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点C、D、E三点在同一直线上,连结BD.求证:
如图,△ACB和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点C、D、E三点在同一直线上,连结BD.求证:(1)BD=CE;
(2)BD⊥CE.
分析 (1)由条件证明△BAD≌△CAE,就可以得到结论;
(2)根据全等三角形的性质得出∠ABD=∠ACE.根据三角形内角和定理求出∠ACE+∠DFC=90°,求出∠FDC=90°即可.
解答 证明:(1)∵△ACB和△ADE都是等腰直角三角形,
∴AE=AD,AB=AC,∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,
即∠BAD=∠CAE,
在△BAD和△CAE中,
$\left\{\begin{array}{l}{AD=AE}\\{∠BAD=∠CAE}\\{AB=AC}\end{array}\right.$,
∴△BAD≌△CAE(SAS),
∴BD=CE;
(2)如图,
∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠CAB=90°,
∴∠ABD+∠AFB=90°,
∴∠ACE+∠AFB=90°,
∵∠DFC=∠AFB,
∴∠ACE+∠DFC=90°,
∴∠FDC=90°,
∴BD⊥CE.
点评 本题考查了全等三角形的判定及性质的运用,垂直的判定及性质的运用,等腰直角三角形的性质的运用,勾股定理的运用,解答时运用全等三角形的性质求解是关键.

练习册系列答案
相关题目
2.正方形ABCD中,在AB边上有一定点E,AE=3cm,EB=1cm,在AC上有一动点P,若使得EP+BP的和最小,则EP+BP的最短距离为( )
| A. | 5cm | B. | 4cm | C. | 3cm | D. | 4.8cm |
4.十二边形的外角和是( )
| A. | 1080° | B. | 1800° | C. | 720° | D. | 360° |
 在一山顶有铁塔AB,从点P到铁塔底部B点有一条索道PB,索道长为300米,与水平线成角为α=30°,在P处测得A点的仰角为β=45°,试求铁塔的高AB.(精确到0.1米,其中$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
在一山顶有铁塔AB,从点P到铁塔底部B点有一条索道PB,索道长为300米,与水平线成角为α=30°,在P处测得A点的仰角为β=45°,试求铁塔的高AB.(精确到0.1米,其中$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)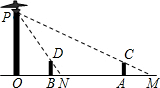 如图,路灯(P点)距地面8米,身高1.6米的小明从距离路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点(B点在A点的左边)时,身影的长度是变长了还是变短了?变长或变短了多少米?
如图,路灯(P点)距地面8米,身高1.6米的小明从距离路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点(B点在A点的左边)时,身影的长度是变长了还是变短了?变长或变短了多少米?