题目内容
11.已知函数y=3(x-2)2+1图象上有三点A(1,y1)、B(4,y2)、C($\sqrt{2}$,y3),试确定y1、y2、y3的大小( )| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y2<y1 | D. | y3<y1<y2 |
分析 先根据二次函数的性质得到抛物线的对称轴为直线x=2,然后比较三个点离直线x=2的远近得到y1、y2、y3的大小关系.
解答 解:∵二次函数的解析式为y=3(x-2)2+1,
∴抛物线的对称轴为直线x=2,
∵A(1,y1)、B(4,y2)、C($\sqrt{2}$,y3),
∴点B离直线x=2最远,点C离直线x=2最近,
而抛物线开口向上,
∴y3<y1<y2.
故选D.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
2.正方形ABCD中,在AB边上有一定点E,AE=3cm,EB=1cm,在AC上有一动点P,若使得EP+BP的和最小,则EP+BP的最短距离为( )
| A. | 5cm | B. | 4cm | C. | 3cm | D. | 4.8cm |
1.学校组织了一次知识竞赛,共有25道题,每一道题答对得5分,答错或不答都扣3分,小明得了85分,那么他答对的题数是( )
| A. | 22 | B. | 20 | C. | 19 | D. | 18 |
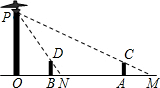 如图,路灯(P点)距地面8米,身高1.6米的小明从距离路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点(B点在A点的左边)时,身影的长度是变长了还是变短了?变长或变短了多少米?
如图,路灯(P点)距地面8米,身高1.6米的小明从距离路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点(B点在A点的左边)时,身影的长度是变长了还是变短了?变长或变短了多少米?