题目内容
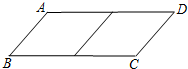 邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作后,余下的四边形是菱形,则称原平行四边形为n阶准菱形.例如:如图,?ABCD中,若AB=1,BC=2,则?ABCD为1阶准菱形.
邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作后,余下的四边形是菱形,则称原平行四边形为n阶准菱形.例如:如图,?ABCD中,若AB=1,BC=2,则?ABCD为1阶准菱形.(1)邻边长分别为2和3的平行四边形是 2阶准菱形吗?说明理由;
(2)操作、探究与计算:
①已知?ABCD的邻边长分别为1,a(a>1),且是3阶准菱形,请画出?ABCD及裁剪线的示意图,并在图形下方写出a的值;
②已知?ABCD的邻边长分别为a,b(a>b),满足a=6b+r,b=5r,请写出?ABCD是几阶准菱形.
考点:四边形综合题
专题:
分析:(1)根据n阶准菱形的定义,当邻边分别为2和3时,可以先剪去一个边长为2的菱形,再剪去一个边长为1的菱形,最后剩下的是一个边长为1的菱形,可得出结论;
(2)①3阶准菱形,可知剪三次菱形,分三个都是相同的菱形,前两次相同,后三次相同和第二次和第三次相同这四种情况来讨论求解即可,
②可知a=31r,b=5r,所以a可以剪5次,b也可以前5次的,故可得出结论.
(2)①3阶准菱形,可知剪三次菱形,分三个都是相同的菱形,前两次相同,后三次相同和第二次和第三次相同这四种情况来讨论求解即可,
②可知a=31r,b=5r,所以a可以剪5次,b也可以前5次的,故可得出结论.
解答:解:(1)是,理由如下:
∵邻边长分别为2和3的平行四边形经过两次操作,所剩四边形是边长为1的菱形,
∴邻边长分别为2和3的平行四边形是2阶准菱形;
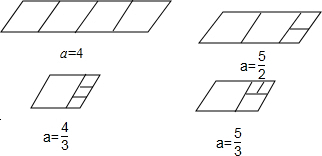
(2)①如图所示,a=4 或a=2.5 或a=
或a=
;
②10阶菱形,
∵a=6b+r,b=5r,
∴a=6×5r+r=31r,如图所示:
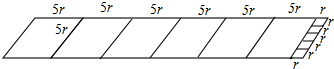
故□ABCD是10阶准菱形.
∵邻边长分别为2和3的平行四边形经过两次操作,所剩四边形是边长为1的菱形,
∴邻边长分别为2和3的平行四边形是2阶准菱形;
(2)①如图所示,a=4 或a=2.5 或a=
| 4 |
| 3 |
| 5 |
| 3 |

②10阶菱形,
∵a=6b+r,b=5r,
∴a=6×5r+r=31r,如图所示:

故□ABCD是10阶准菱形.
点评:本题主要考查对新概念的理解及菱形的判定,正确理解题目中所给出的n阶准菱形的概念是解题的关键.

练习册系列答案
相关题目
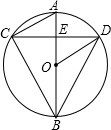 如图,已知:在⊙O中,AB是⊙O的直径,弦CD垂直平分OA,垂足为E,连接AC、BC、BD、OD.
如图,已知:在⊙O中,AB是⊙O的直径,弦CD垂直平分OA,垂足为E,连接AC、BC、BD、OD.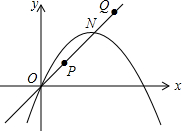 已知抛物线y=-
已知抛物线y=-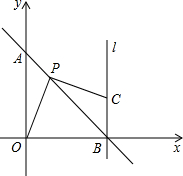 如图,在平面直角坐标系xOy中,A、B的坐标分别是(0,4)、(4,0).
如图,在平面直角坐标系xOy中,A、B的坐标分别是(0,4)、(4,0).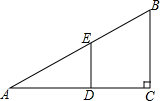 在Rt△ABC中,∠ACB=90°,BC=3,AC=4,D、E分别为AC和AB上的一个动点,则BD+DE的最小值是
在Rt△ABC中,∠ACB=90°,BC=3,AC=4,D、E分别为AC和AB上的一个动点,则BD+DE的最小值是