题目内容
一个圆的半径为6,则它的内接正三角形与外切正三角形的面积比为 .
考点:正多边形和圆
专题:
分析:根据题意画出图形,先求出正三角形的中心角及边心距,再根据三角形的面积公式求解即可.
解答: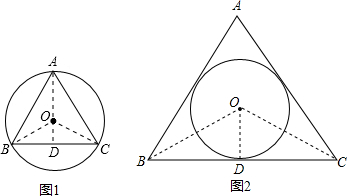 解:如图1所示,过O作OD⊥BC于D;
解:如图1所示,过O作OD⊥BC于D;
∵此三角形是正三角形,
∴∠BOC=360°÷3=120°.
∵OB=OC,
∴∠BOD=
×120°=60°,
∴∠OBD=30°;
∵OB=6,
∴OD=
OB=3,BD=OB•cos30°=6×
=3
,
∴BC=2BD=2×3
=6
,
∴S△BOC=
×BC×OD=
×6
×3=9
,
∴S△ABC=3×9
=27
.
如图2所示,
∵此三角形是正三角形,
∴∠BOC=360°÷3=120°.
∵OB=OC,
∴∠BOD=
×120°=60°,
∴∠OBD=30°;
∵OD=6,
∴BD=
=
=6
,
∴BC=2BD=2×6
=12
,
∴S△BOC=
×BC×OD=
×12
×6=36
,
∴S△ABC=3×36
=108
.
∴
=
=
.
故答案为:1:4.
 解:如图1所示,过O作OD⊥BC于D;
解:如图1所示,过O作OD⊥BC于D;∵此三角形是正三角形,
∴∠BOC=360°÷3=120°.
∵OB=OC,
∴∠BOD=
| 1 |
| 2 |
∴∠OBD=30°;
∵OB=6,
∴OD=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴BC=2BD=2×3
| 3 |
| 3 |
∴S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴S△ABC=3×9
| 3 |
| 3 |
如图2所示,
∵此三角形是正三角形,
∴∠BOC=360°÷3=120°.
∵OB=OC,
∴∠BOD=
| 1 |
| 2 |
∴∠OBD=30°;
∵OD=6,
∴BD=
| OD |
| tan30° |
| 6 | ||||
|
| 3 |
∴BC=2BD=2×6
| 3 |
| 3 |
∴S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴S△ABC=3×36
| 3 |
| 3 |
∴
| S内接三角形 |
| S外切三角形 |
27
| ||
108
|
| 1 |
| 4 |
故答案为:1:4.
点评:本题考查的是正多边形和圆,熟知正三角形的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
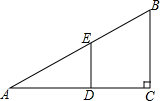 在Rt△ABC中,∠ACB=90°,BC=3,AC=4,D、E分别为AC和AB上的一个动点,则BD+DE的最小值是
在Rt△ABC中,∠ACB=90°,BC=3,AC=4,D、E分别为AC和AB上的一个动点,则BD+DE的最小值是 如图,在正方形ABCD中,E为AD中点,G为DC上一点,且DG=
如图,在正方形ABCD中,E为AD中点,G为DC上一点,且DG=