题目内容
5.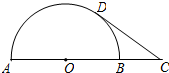 如图,AB是半圆的直径,点O是圆心,点C是AB延长线的一点,CD与半圆相切于点D.若AB=6,CD=4,则sin∠C的值为( )
如图,AB是半圆的直径,点O是圆心,点C是AB延长线的一点,CD与半圆相切于点D.若AB=6,CD=4,则sin∠C的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{3}$ |
分析 根据切线的性质得到△OCD是直角三角形,由勾股定理求得OC的长度,即可得到结果.
解答  解:连接OD,
解:连接OD,
∵AB是半圆的直径,AB=6,
∴OD=3,
∵CD与半圆相切于点D,
∴∠CDO=90°,
∵CD=4,
∴OC=$\sqrt{C{D}^{2}+O{D}^{2}}$=5,
∴sin∠C=$\frac{OD}{OC}$=$\frac{3}{5}$,
故选B.
点评 本题考查了切线的性质,勾股定理,锐角三角函数的求法,作辅助线构造直角三角形是解题的关键.

练习册系列答案
相关题目
13.用火柴棒按下列方式搭建三角形:

(1)填表:
(2)当三角形的个数为n时,火柴棒的根数是多少?(用含n的式子表示)
(3)求当n=100时,火柴棒的根数是多少?
(4)当火柴棒的根数为2013时,三角形的个数是多少?

(1)填表:
| 三角形个数 | 1 | 2 | 3 | 4 | 5 |
| 火柴棒根数 | 3 | 5 | 7 | 9 | 11 |
(3)求当n=100时,火柴棒的根数是多少?
(4)当火柴棒的根数为2013时,三角形的个数是多少?
10.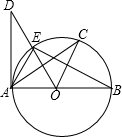 如图,AB是⊙O的直径,AD切⊙O于点A,$\widehat{EC}$=$\widehat{CB}$.则下列结论:①BA⊥DA;②OC∥AE;③∠COE=2∠CAE;④OD⊥AC,一定正确的个数有( )
如图,AB是⊙O的直径,AD切⊙O于点A,$\widehat{EC}$=$\widehat{CB}$.则下列结论:①BA⊥DA;②OC∥AE;③∠COE=2∠CAE;④OD⊥AC,一定正确的个数有( )
 如图,AB是⊙O的直径,AD切⊙O于点A,$\widehat{EC}$=$\widehat{CB}$.则下列结论:①BA⊥DA;②OC∥AE;③∠COE=2∠CAE;④OD⊥AC,一定正确的个数有( )
如图,AB是⊙O的直径,AD切⊙O于点A,$\widehat{EC}$=$\widehat{CB}$.则下列结论:①BA⊥DA;②OC∥AE;③∠COE=2∠CAE;④OD⊥AC,一定正确的个数有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
15. 如图,直线l1∥l2,∠2=65°,∠3=60°,则∠1为( )
如图,直线l1∥l2,∠2=65°,∠3=60°,则∠1为( )
 如图,直线l1∥l2,∠2=65°,∠3=60°,则∠1为( )
如图,直线l1∥l2,∠2=65°,∠3=60°,则∠1为( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
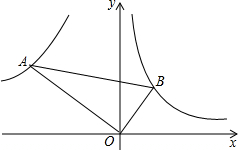 如图所示,Rt△AOB中,∠AOB=90°,OA=10,点B在反比例函数y=$\frac{12}{x}$图象上,且点B的横坐标为3.
如图所示,Rt△AOB中,∠AOB=90°,OA=10,点B在反比例函数y=$\frac{12}{x}$图象上,且点B的横坐标为3.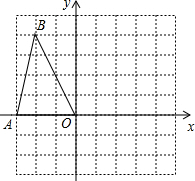 如图,正方形网格中的每一个小正方形的边长都是1,△AOB的三个顶点都在格点上,以O为坐标原点,建立如图平面直角坐标系,若把△AOB绕着点O顺时针旋转90°,得到△A1OB1,则点B旋转后的对应点B1的坐标为(4,2).
如图,正方形网格中的每一个小正方形的边长都是1,△AOB的三个顶点都在格点上,以O为坐标原点,建立如图平面直角坐标系,若把△AOB绕着点O顺时针旋转90°,得到△A1OB1,则点B旋转后的对应点B1的坐标为(4,2).