题目内容
10.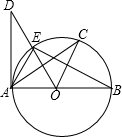 如图,AB是⊙O的直径,AD切⊙O于点A,$\widehat{EC}$=$\widehat{CB}$.则下列结论:①BA⊥DA;②OC∥AE;③∠COE=2∠CAE;④OD⊥AC,一定正确的个数有( )
如图,AB是⊙O的直径,AD切⊙O于点A,$\widehat{EC}$=$\widehat{CB}$.则下列结论:①BA⊥DA;②OC∥AE;③∠COE=2∠CAE;④OD⊥AC,一定正确的个数有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
分析 分别根据切线的性质、平行线的判定定理及圆周角定理对各选项进行逐一判断即可.
解答 解:∵AB是⊙O的直径,AD切⊙O于点A,
∴BA⊥DA,故①正确;
$\widehat{EC}=\widehat{BC}$,
∴∠EAC=∠CAB,
∵OA=OC,
∴∠CAB=∠ACO,
∴∠EAC=∠ACO,
∴OC∥AE,故②正确;
∵∠COE是$\widehat{CE}$所对的圆心角,∠CAE是$\widehat{CE}$所对的圆周角,
∴∠COE=2∠CAE,故③正确;
只有当$\widehat{AE}$=$\widehat{CE}$时,OD⊥AC,故④错误.
故选A.
点评 本题考查的是切线的性质,圆周角定理及圆心角、弧、弦的关系,熟知圆的切线垂直于经过切点的半径是解答此题的关键.

练习册系列答案
相关题目
17.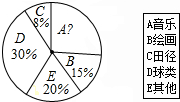 某初中为了了解初中学生课余时间最喜欢的文体活动,学生会在本校初中学生中随机调查了部分学生最喜欢的文体活动项目:A音乐,B绘画,C田径,D球类,E其他(被调查对象选且只选其中的一项),对调查结果进行整理,并制作了不完整的统计表和统计图(如图所示):
某初中为了了解初中学生课余时间最喜欢的文体活动,学生会在本校初中学生中随机调查了部分学生最喜欢的文体活动项目:A音乐,B绘画,C田径,D球类,E其他(被调查对象选且只选其中的一项),对调查结果进行整理,并制作了不完整的统计表和统计图(如图所示):
“最喜欢的文体活动”调查统计表
(1)根据统计表和图中的信息将“统计表”填写完整;
(2)若该校共有初中学生900人,请你估计该校最喜欢“A音乐”的人数约有多少人?
 某初中为了了解初中学生课余时间最喜欢的文体活动,学生会在本校初中学生中随机调查了部分学生最喜欢的文体活动项目:A音乐,B绘画,C田径,D球类,E其他(被调查对象选且只选其中的一项),对调查结果进行整理,并制作了不完整的统计表和统计图(如图所示):
某初中为了了解初中学生课余时间最喜欢的文体活动,学生会在本校初中学生中随机调查了部分学生最喜欢的文体活动项目:A音乐,B绘画,C田径,D球类,E其他(被调查对象选且只选其中的一项),对调查结果进行整理,并制作了不完整的统计表和统计图(如图所示):“最喜欢的文体活动”调查统计表
| 项目 | A音乐 | B绘画 | C田径 | D球类 | E其他 |
| 频数 | 正正正正正正 | ||||
| 人数(人) | 20 |
(2)若该校共有初中学生900人,请你估计该校最喜欢“A音乐”的人数约有多少人?
1.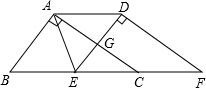 如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,将△ABC沿直线BC方向平移2.5个单位得到△DEF,AC与DE相交于G点,连接AD,AE,则下列结论:
如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,将△ABC沿直线BC方向平移2.5个单位得到△DEF,AC与DE相交于G点,连接AD,AE,则下列结论:
①△AGD≌△CGE;②△ADE为等腰三角形;③AC平分∠EAD;④四边形AEFD的面积为9.
其中正确的个数是( )
 如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,将△ABC沿直线BC方向平移2.5个单位得到△DEF,AC与DE相交于G点,连接AD,AE,则下列结论:
如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,将△ABC沿直线BC方向平移2.5个单位得到△DEF,AC与DE相交于G点,连接AD,AE,则下列结论:①△AGD≌△CGE;②△ADE为等腰三角形;③AC平分∠EAD;④四边形AEFD的面积为9.
其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.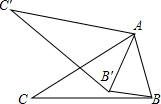 如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( )
如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( )
 如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( )
如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
5.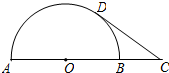 如图,AB是半圆的直径,点O是圆心,点C是AB延长线的一点,CD与半圆相切于点D.若AB=6,CD=4,则sin∠C的值为( )
如图,AB是半圆的直径,点O是圆心,点C是AB延长线的一点,CD与半圆相切于点D.若AB=6,CD=4,则sin∠C的值为( )
 如图,AB是半圆的直径,点O是圆心,点C是AB延长线的一点,CD与半圆相切于点D.若AB=6,CD=4,则sin∠C的值为( )
如图,AB是半圆的直径,点O是圆心,点C是AB延长线的一点,CD与半圆相切于点D.若AB=6,CD=4,则sin∠C的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{3}$ |
15.已知点A(a-3b,2-6ab)在抛物线y=x2+6x+20上,则点A关于x轴的对称点坐标为( )
| A. | (6,20) | B. | (-6,20) | C. | (6,-20) | D. | (-6,-20) |
20.某商场将一件玩具按进价提高60%后标价,销售时按标价打折销售,结果相对于进价仍获利20%,则这件玩具销售时打的折扣是( )
| A. | 8折 | B. | 7.5折 | C. | 6折 | D. | 3.3折 |
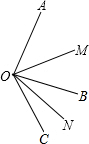 如图,已知∠AOB=80°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.
如图,已知∠AOB=80°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC. 如图是一次函数y=2x-5的图象,请根据给出的图象写出一个一元一次方程和一个一元一次不等式,并用图象求解所写出的方程和不等式.
如图是一次函数y=2x-5的图象,请根据给出的图象写出一个一元一次方程和一个一元一次不等式,并用图象求解所写出的方程和不等式.