题目内容
20.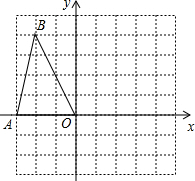 如图,正方形网格中的每一个小正方形的边长都是1,△AOB的三个顶点都在格点上,以O为坐标原点,建立如图平面直角坐标系,若把△AOB绕着点O顺时针旋转90°,得到△A1OB1,则点B旋转后的对应点B1的坐标为(4,2).
如图,正方形网格中的每一个小正方形的边长都是1,△AOB的三个顶点都在格点上,以O为坐标原点,建立如图平面直角坐标系,若把△AOB绕着点O顺时针旋转90°,得到△A1OB1,则点B旋转后的对应点B1的坐标为(4,2).
分析 作BC⊥y轴,B1D⊥x轴,根据△BOC≌△B1OD,求出OD、B1D的长,得到答案.
解答 解: 如图,作BC⊥y轴,B1D⊥x轴,
如图,作BC⊥y轴,B1D⊥x轴,
由题意得,△BOC≌△B1OD,
∴OD=OC=4,B1D=BC=2,
∴点B1的坐标为:(4,2),
故答案为:(4,2).
点评 本题考查的是旋转的旋转和三角形全等的性质,正确理解旋转的旋转中心、旋转角和旋转分析是解题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
7.若$\frac{a+b}{c}$=$\frac{b+c}{a}$=$\frac{a+c}{b}$=k,则一次函数y=kx+x必经过( )
| A. | 第一、二象限 | B. | 第二、三象限 | C. | 第三、四象限 | D. | 第一、四象限 |
15.已知等腰三角形的两边长分别为5cm、3cm,则该等腰三角形的周长是( )
| A. | 13cm | B. | 11cm | C. | 13cm或者11cm | D. | 8cm |
5.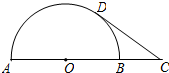 如图,AB是半圆的直径,点O是圆心,点C是AB延长线的一点,CD与半圆相切于点D.若AB=6,CD=4,则sin∠C的值为( )
如图,AB是半圆的直径,点O是圆心,点C是AB延长线的一点,CD与半圆相切于点D.若AB=6,CD=4,则sin∠C的值为( )
 如图,AB是半圆的直径,点O是圆心,点C是AB延长线的一点,CD与半圆相切于点D.若AB=6,CD=4,则sin∠C的值为( )
如图,AB是半圆的直径,点O是圆心,点C是AB延长线的一点,CD与半圆相切于点D.若AB=6,CD=4,则sin∠C的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{3}$ |
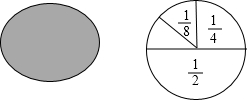 小梅在餐厅吃饭时,发现了一个有趣的问题:厨师喜欢将做好的油饼都切成一个个小扇形.小梅在想:如果第一次切去圆饼的一半,第二次切去剩余的一半,第三次继续切去剩余的一半,…(如图所示):
小梅在餐厅吃饭时,发现了一个有趣的问题:厨师喜欢将做好的油饼都切成一个个小扇形.小梅在想:如果第一次切去圆饼的一半,第二次切去剩余的一半,第三次继续切去剩余的一半,…(如图所示):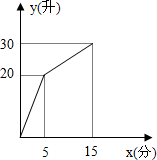 某数学课外活动小组利用一个有进水管与出水管的容器模拟水池蓄水情况:从某时刻开始,5分钟内只进水不出水,在随后的10分钟内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的蓄水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则第12分钟容器内的蓄水量为( )
某数学课外活动小组利用一个有进水管与出水管的容器模拟水池蓄水情况:从某时刻开始,5分钟内只进水不出水,在随后的10分钟内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的蓄水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则第12分钟容器内的蓄水量为( )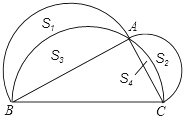 在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作$\widehat{BAC}$,如图,S1、S2、S3、S4分别表示图中四个“月牙形”的面积.若AB=4,AC=2,S1-S2=$\frac{π}{4}$,则S3-S4的值是$\frac{5}{4}$π.
在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作$\widehat{BAC}$,如图,S1、S2、S3、S4分别表示图中四个“月牙形”的面积.若AB=4,AC=2,S1-S2=$\frac{π}{4}$,则S3-S4的值是$\frac{5}{4}$π. 三棱柱的三视图如图所示,在△EFG中,FG=18cm,EG=14cm,∠EGF=30°,则AB的长为7cm.
三棱柱的三视图如图所示,在△EFG中,FG=18cm,EG=14cm,∠EGF=30°,则AB的长为7cm.