题目内容
17.若x2-5x+1=0,求2x2-9x-3+$\frac{5}{{x}^{2}+1}$的值.分析 首先根据x2-5x+1=0,可得x2=5x-1,然后把x2=5x-1代入算式2x2-9x-3+$\frac{5}{{x}^{2}+1}$,求出算式2x2-9x-3+$\frac{5}{{x}^{2}+1}$的值是多即可.
解答 解:∵x2-5x+1=0,
∴x2=5x-1,
2x2-9x-3+$\frac{5}{{x}^{2}+1}$
=2×(5x-1)-9x-3+$\frac{5}{{x}^{2}+1}$
=10x-2-9x-3+$\frac{5}{5x}$
=x-5+$\frac{1}{x}$
=$\frac{{x}^{2}-5x+1}{x}$
=$\frac{0}{x}$
=0
点评 此题主要考查了分式的化简求值问题,注意化简时不能跨度太大,而缺少必要的步骤,解答此题的关键是要明确:代入求值时,有直接代入法,整体代入法等常用方法.解题时可根据题目的具体条件选择合适的方法.当未知数的值没有明确给出时,所选取的未知数的值必须使原式中的各分式都有意义,且除数不能为0.

练习册系列答案
相关题目
5.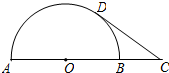 如图,AB是半圆的直径,点O是圆心,点C是AB延长线的一点,CD与半圆相切于点D.若AB=6,CD=4,则sin∠C的值为( )
如图,AB是半圆的直径,点O是圆心,点C是AB延长线的一点,CD与半圆相切于点D.若AB=6,CD=4,则sin∠C的值为( )
 如图,AB是半圆的直径,点O是圆心,点C是AB延长线的一点,CD与半圆相切于点D.若AB=6,CD=4,则sin∠C的值为( )
如图,AB是半圆的直径,点O是圆心,点C是AB延长线的一点,CD与半圆相切于点D.若AB=6,CD=4,则sin∠C的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{3}$ |
12.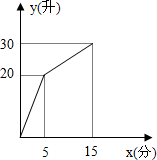 某数学课外活动小组利用一个有进水管与出水管的容器模拟水池蓄水情况:从某时刻开始,5分钟内只进水不出水,在随后的10分钟内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的蓄水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则第12分钟容器内的蓄水量为( )
某数学课外活动小组利用一个有进水管与出水管的容器模拟水池蓄水情况:从某时刻开始,5分钟内只进水不出水,在随后的10分钟内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的蓄水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则第12分钟容器内的蓄水量为( )
 某数学课外活动小组利用一个有进水管与出水管的容器模拟水池蓄水情况:从某时刻开始,5分钟内只进水不出水,在随后的10分钟内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的蓄水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则第12分钟容器内的蓄水量为( )
某数学课外活动小组利用一个有进水管与出水管的容器模拟水池蓄水情况:从某时刻开始,5分钟内只进水不出水,在随后的10分钟内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的蓄水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则第12分钟容器内的蓄水量为( )| A. | 22 | B. | 25 | C. | 27 | D. | 28 |
6. 如图,AB∥CD,BE交CD于点F,若∠B=50°,则∠DFE的度数为( )
如图,AB∥CD,BE交CD于点F,若∠B=50°,则∠DFE的度数为( )
 如图,AB∥CD,BE交CD于点F,若∠B=50°,则∠DFE的度数为( )
如图,AB∥CD,BE交CD于点F,若∠B=50°,则∠DFE的度数为( )| A. | 40° | B. | 50° | C. | 130° | D. | 150° |
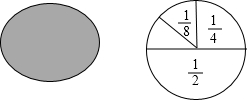 小梅在餐厅吃饭时,发现了一个有趣的问题:厨师喜欢将做好的油饼都切成一个个小扇形.小梅在想:如果第一次切去圆饼的一半,第二次切去剩余的一半,第三次继续切去剩余的一半,…(如图所示):
小梅在餐厅吃饭时,发现了一个有趣的问题:厨师喜欢将做好的油饼都切成一个个小扇形.小梅在想:如果第一次切去圆饼的一半,第二次切去剩余的一半,第三次继续切去剩余的一半,…(如图所示):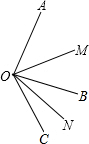 如图,已知∠AOB=80°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.
如图,已知∠AOB=80°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.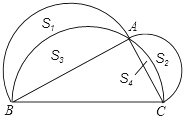 在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作$\widehat{BAC}$,如图,S1、S2、S3、S4分别表示图中四个“月牙形”的面积.若AB=4,AC=2,S1-S2=$\frac{π}{4}$,则S3-S4的值是$\frac{5}{4}$π.
在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作$\widehat{BAC}$,如图,S1、S2、S3、S4分别表示图中四个“月牙形”的面积.若AB=4,AC=2,S1-S2=$\frac{π}{4}$,则S3-S4的值是$\frac{5}{4}$π.