题目内容
11.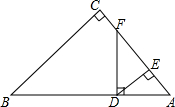 如图所示,在△ABC中,∠C=90°,D是AB上一点,DF⊥AB交AC于点F,DE⊥AC,垂足为点E.若EF:CF=2:1,DE=2,BD=6$\sqrt{5}$,求BC的长.
如图所示,在△ABC中,∠C=90°,D是AB上一点,DF⊥AB交AC于点F,DE⊥AC,垂足为点E.若EF:CF=2:1,DE=2,BD=6$\sqrt{5}$,求BC的长.
分析 过FG∥BC交AB于G,推出FG∥DE,由EF:CF=2:1,设CF=k,EF=2k,得到BG:DG=CF:EF=1:2,求出BG=2$\sqrt{5}$,DG=4$\sqrt{5}$,通过△DGF∽△EFD,得到$\frac{DG}{EF}=\frac{DF}{DE}$,解得DF=$\frac{4\sqrt{5}}{k}$,在Rt△EFD中,DF2=DE2+EF2,列方程求得k=2,得到CF=2,EF=4,DF=2$\sqrt{5}$,由射影定理得:DF2=EF•AF,求出AF=$\frac{D{F}^{2}}{EF}$=5,根据勾股定理即可得到结论.
解答 解:过FG∥BC交AB于G,
∵∠C=90°,DE⊥AC,
∴DE∥BC,
∴FG∥DE,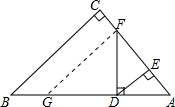
∵EF:CF=2:1,
设CF=k,EF=2k,
∴BG:DG=CF:EF=1:2,
∵BD=6$\sqrt{5}$,
∴BG=2$\sqrt{5}$,DG=4$\sqrt{5}$,
∵DF⊥AB,
∴∠FDG=∠DEF=90°,
∵∠GFD=∠FDE,
∴△DGF∽△EFD,
∴$\frac{DG}{EF}=\frac{DF}{DE}$,
即$\frac{4\sqrt{5}}{2k}=\frac{DF}{2}$,
∴DF=$\frac{4\sqrt{5}}{k}$,
在Rt△EFD中,DF2=DE2+EF2,
即($\frac{4\sqrt{5}}{k}$)2=22+(2k)2,
解得:k=2,(负值舍去),
∴CF=2,EF=4,DF=2$\sqrt{5}$,
由射影定理得:DF2=EF•AF,
∴AF=$\frac{D{F}^{2}}{EF}$=5,
∴AD=$\sqrt{A{F}^{2}-D{F}^{2}}$=$\sqrt{5}$,
∴AB=7$\sqrt{5}$,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=14.
点评 本题考查了相似三角形的判定和性质,直角三角形的性质,平行线的性质,勾股定理,射影定理,正确的作出辅助线是解题的关键.

 名校课堂系列答案
名校课堂系列答案 如图,已知∠3=∠4,要得到AB∥CD,需要添加的条件是( )
如图,已知∠3=∠4,要得到AB∥CD,需要添加的条件是( )| A. | ∠1=∠4 | B. | ∠3=∠2 | C. | ∠1=∠2 | D. | ∠1与∠2互补 |
 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,∠A=120°,BD平分∠ABC,则∠BDC=90°.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,∠A=120°,BD平分∠ABC,则∠BDC=90°. 如图所示,有一抛物线形门洞,地面宽度为8m,有一宽6m,高4m的车刚好能通过这个门洞,求这个门洞的高度.(精确到0.01m)
如图所示,有一抛物线形门洞,地面宽度为8m,有一宽6m,高4m的车刚好能通过这个门洞,求这个门洞的高度.(精确到0.01m) 如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,CD与AB的延长线相交于点D,∠CAD=20°,则∠D=50°.
如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,CD与AB的延长线相交于点D,∠CAD=20°,则∠D=50°.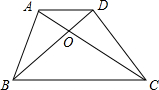 如图,四边形ABCD的对角线AC,BD相交于点0,且∠BAO=∠CDO,试问$\frac{AD}{BC}$=$\frac{AO}{BO}$成立吗?并说明理由.
如图,四边形ABCD的对角线AC,BD相交于点0,且∠BAO=∠CDO,试问$\frac{AD}{BC}$=$\frac{AO}{BO}$成立吗?并说明理由.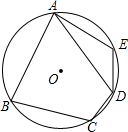 在⊙O的内接四边形ABCD中,AB=AD,∠C=110°,若点E在$\widehat{AD}$上,求∠E的度数.
在⊙O的内接四边形ABCD中,AB=AD,∠C=110°,若点E在$\widehat{AD}$上,求∠E的度数.