题目内容
19. 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,∠A=120°,BD平分∠ABC,则∠BDC=90°.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,∠A=120°,BD平分∠ABC,则∠BDC=90°.
分析 由等腰梯形的性质得出∠ADC=∠A=120°,∠A+∠ABC=180°,∠ADB=∠CBD,求出∠CBD=30°,得出∠ADB,即可得出∠BDC的度数.
解答 解:∵四边形ABCD是等腰梯形,AD∥BC,
∴∠ADC=∠A=120°,∠A+∠ABC=180°,∠ADB=∠CBD,
∴∠ABC=60°,
∵BD平分∠ABC,
∴∠CBD=$\frac{1}{2}$∠ABC=30°,
∴∠ADB=30°,
∴∠BDC=∠ADC-∠ADB=90°;
故答案为:90°.
点评 本题考查了等腰梯形的性质、平行线的性质、角平分线的定义;熟练掌握等腰梯形的性质,由角平分线和平行线的性质求出∠ADB的度数是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,∠C=90°,∠1=∠2,若BC=9,BD=5,则D到AB的距离为4.
如图,∠C=90°,∠1=∠2,若BC=9,BD=5,则D到AB的距离为4.
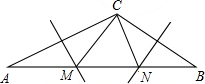 如图,在△ABC中,∠ACB=130°,AC、BC的垂直平分线分别交AB于点M、N,则∠MCN=80°.
如图,在△ABC中,∠ACB=130°,AC、BC的垂直平分线分别交AB于点M、N,则∠MCN=80°.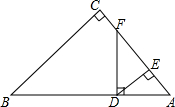 如图所示,在△ABC中,∠C=90°,D是AB上一点,DF⊥AB交AC于点F,DE⊥AC,垂足为点E.若EF:CF=2:1,DE=2,BD=6$\sqrt{5}$,求BC的长.
如图所示,在△ABC中,∠C=90°,D是AB上一点,DF⊥AB交AC于点F,DE⊥AC,垂足为点E.若EF:CF=2:1,DE=2,BD=6$\sqrt{5}$,求BC的长.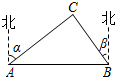 如图,A,B两市相距150千米,分别从A,B处测得风景区中心C处的方向角如图所示,风景区区域是以C为圆心,45千米为半径的圆.现计划修建连接A,B两市的笔直高速公路,此高速公路是否穿过风景区,请说明理由(tanα=1.627,tanβ=1.373).
如图,A,B两市相距150千米,分别从A,B处测得风景区中心C处的方向角如图所示,风景区区域是以C为圆心,45千米为半径的圆.现计划修建连接A,B两市的笔直高速公路,此高速公路是否穿过风景区,请说明理由(tanα=1.627,tanβ=1.373). 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则$\widehat{AC}$的长π.
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则$\widehat{AC}$的长π.