题目内容
1.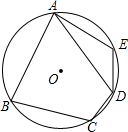 在⊙O的内接四边形ABCD中,AB=AD,∠C=110°,若点E在$\widehat{AD}$上,求∠E的度数.
在⊙O的内接四边形ABCD中,AB=AD,∠C=110°,若点E在$\widehat{AD}$上,求∠E的度数.
分析 连接BD,先根据圆内接四边形的性质计算出∠BAD=180°-∠C=70°,再根据等腰三角形的性质和三角形内角和定理计算出∠ABD=55°,然后再根据圆内接四边形的性质可得∠E的度数.
解答  解:连接BD,
解:连接BD,
∵∠C+∠BAD=180°,
∴∠BAD=180°-110°=70°,
∵AB=AD,
∴∠ABD=∠ADB,
∴∠ABD=$\frac{1}{2}$(180°-70°)=55°,
∵四边形ABDE为圆的内接四边形,
∴∠E+∠ABD=180°,
∴∠E=180°-55°=125°.
点评 本题考查了圆内接四边形的性质以及等腰三角形的性质,关键是掌握圆内接四边形的对角互补.

练习册系列答案
相关题目
12.下列命题错误的是( )
| A. | 相似三角形周长之比等于对应高之比 | |
| B. | 两个等腰直角三角形一定相似 | |
| C. | 各有一个角等于91°的两个等腰三角形相似 | |
| D. | 两边对应成比例且有一个角相等的两个三角形相似 |
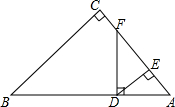 如图所示,在△ABC中,∠C=90°,D是AB上一点,DF⊥AB交AC于点F,DE⊥AC,垂足为点E.若EF:CF=2:1,DE=2,BD=6$\sqrt{5}$,求BC的长.
如图所示,在△ABC中,∠C=90°,D是AB上一点,DF⊥AB交AC于点F,DE⊥AC,垂足为点E.若EF:CF=2:1,DE=2,BD=6$\sqrt{5}$,求BC的长. 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则$\widehat{AC}$的长π.
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则$\widehat{AC}$的长π.