题目内容
20.已知三条直线L1:(m-2)x-y=1、L2:x-y=3、L3:2x-y=2相交于同一点,则m=( )| A. | 6 | B. | 5 | C. | 4 | D. | -3 |
分析 由L2和L3的解析式可求得交点坐标,再把交点坐标代入L1可求得m的值.
解答 解:联立L2和L3的解析式可得$\left\{\begin{array}{l}{x-y=3}\\{2x-y=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-1}\\{y=-4}\end{array}\right.$,
∴三条直线的交点坐标为(-1,-4),
又∵直线L1过交点,
∴-(m-2)-(-4)=1,解得m=5,
故选B.
点评 本题主要考查两直线的交点问题,掌握求函数图象的交点问题的方法(即联立函数解析式构成方程组,求方程组的解)是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.若$\sqrt{x-1}$的在实数范围内有意义,则( )
| A. | x≥1 | B. | x≠1 | C. | x>1 | D. | x≤1 |
12.直角三角形的两条直角边长为3和4,则该直角三角形斜边上的高为( )
| A. | 5 | B. | 7 | C. | $\frac{12}{5}$ | D. | $\frac{24}{5}$ |
10.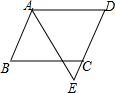 如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交DC的延长线于点E,CE的长为( )
如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交DC的延长线于点E,CE的长为( )
 如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交DC的延长线于点E,CE的长为( )
如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交DC的延长线于点E,CE的长为( )| A. | 2 | B. | 3 | C. | 4 | D. | 2.5 |
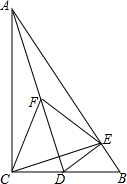 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,D为BC上一点,过点D作DE⊥AB于E.
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,D为BC上一点,过点D作DE⊥AB于E.