题目内容
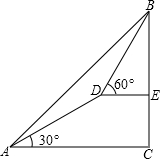 某测量对在山脚A处测得山上树顶仰角为45°(如图),测量队在上坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,求山高为多少米?(精确到1米,
某测量对在山脚A处测得山上树顶仰角为45°(如图),测量队在上坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,求山高为多少米?(精确到1米,| 3 |
考点:解直角三角形的应用-仰角俯角问题,解直角三角形的应用-坡度坡角问题
专题:
分析:过点D作DE⊥AC,可得到△ACB是等腰直角三角形,直角△ADE中满足解直角三角形的条件.可以设EC=x,在直角△BDF中,根据勾股定理,可以用x表示出BF,根据AC=BC就可以得到关于x的方程,就可以求出x,得到BC,求出山高.
解答: 解:过点D作DF⊥AC于F.
解:过点D作DF⊥AC于F.
在直角△ADF中,AF=AD•cos30°=300
米,DF=
AD=300米.
设FC=x,则AC=300
+x.
在直角△BDE中,BE=
DE=
x,则BC=300+
x.
在直角△ACB中,∠BAC=45°.
∴这个三角形是等腰直角三角形.
∴AC=BC.
∴300
+x=300+
x.
解得:x=300.
∴BC=AC=300+300
.
∴山高是300+300
-15=285+300
≈805(米).
 解:过点D作DF⊥AC于F.
解:过点D作DF⊥AC于F.在直角△ADF中,AF=AD•cos30°=300
| 3 |
| 1 |
| 2 |
设FC=x,则AC=300
| 3 |
在直角△BDE中,BE=
| 3 |
| 3 |
| 3 |
在直角△ACB中,∠BAC=45°.
∴这个三角形是等腰直角三角形.
∴AC=BC.
∴300
| 3 |
| 3 |
解得:x=300.
∴BC=AC=300+300
| 3 |
∴山高是300+300
| 3 |
| 3 |
点评:本题考查了解直角三角形的应用.此题的难度较大,建立数学模型是关键.根据勾股定理,把问题转化为方程问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题是真命题的是( )
| A、等边对等角 |
| B、周长相等的两个等腰三角形全等 |
| C、等腰三角形的角平分线、中线和高线互相重合 |
| D、三角形一条边的两个顶点到这条边上的中线所在直线的距离相等 |
关于双曲线y=-
的图象,以下说法正确的是( )
| 3 |
| x |
| A、双曲线的两支既关于x的轴对称又关于y轴对称 |
| B、双曲线的两支既不关于x轴对称又不关于y轴对称 |
| C、双曲线的两支不关于x轴对称但关于y轴对称 |
| D、双曲线的两支关于x轴对称但不关于y轴对称 |
 如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于O,S△ADO=1,S△DCO=4,则△AOD与△BOC的面积比等于( )
如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于O,S△ADO=1,S△DCO=4,则△AOD与△BOC的面积比等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
点A(-2,3)关于x轴的对称点A′的坐标为( )
| A、(2,-3) |
| B、(-2,-3) |
| C、(-2,3) |
| D、( 2,3) |
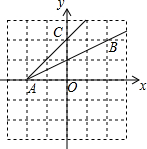 如图,已知点A(-2,0),B(2,2),C(0,2),则tan∠BAC=
如图,已知点A(-2,0),B(2,2),C(0,2),则tan∠BAC= 如图,在Rt△AOB中,OB=1,AB=2,以原点O为圆心,OA为半径画弧,交数轴于点P,则点P表示的实数是
如图,在Rt△AOB中,OB=1,AB=2,以原点O为圆心,OA为半径画弧,交数轴于点P,则点P表示的实数是