题目内容
 如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于O,S△ADO=1,S△DCO=4,则△AOD与△BOC的面积比等于( )
如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于O,S△ADO=1,S△DCO=4,则△AOD与△BOC的面积比等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:相似三角形的判定与性质,梯形
专题:
分析:由等高三角形的面积的比等于对应底的比,可求得△AOB与△COD的面积,再根据梯形ABCD中AD∥BC,可得△AOD∽△COB,然后由相似三角形面积比等于相似比的平方,继而求得答案.
解答:解:∵S△ADO=1,S△DCO=4,
∴AO:CO=1:4
∵梯形ABCD中AD∥BC,
∴△AOD∽△COB,
∴S△AOD:S△BOC=1:16,
故选D.
∴AO:CO=1:4
∵梯形ABCD中AD∥BC,
∴△AOD∽△COB,
∴S△AOD:S△BOC=1:16,
故选D.
点评:此题考查了梯形的性质以及相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
 如图所示,△ABC为⊙O的内接三角形,AB=1,∠C=30°,则⊙O的内接六边形的面积为( )
如图所示,△ABC为⊙O的内接三角形,AB=1,∠C=30°,则⊙O的内接六边形的面积为( )A、
| ||||
B、6
| ||||
| C、8 | ||||
| D、16 |
 如图是两个可以自由转动的转盘,每个转盘被分成两个扇形,同时转动两个转盘,转盘停止后,指针所指区域内的数字之和为偶数的概率是( )
如图是两个可以自由转动的转盘,每个转盘被分成两个扇形,同时转动两个转盘,转盘停止后,指针所指区域内的数字之和为偶数的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
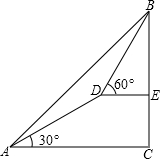 某测量对在山脚A处测得山上树顶仰角为45°(如图),测量队在上坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,求山高为多少米?(精确到1米,
某测量对在山脚A处测得山上树顶仰角为45°(如图),测量队在上坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,求山高为多少米?(精确到1米,