题目内容
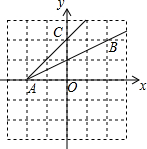 如图,已知点A(-2,0),B(2,2),C(0,2),则tan∠BAC=
如图,已知点A(-2,0),B(2,2),C(0,2),则tan∠BAC=考点:勾股定理的逆定理,坐标与图形性质,勾股定理,锐角三角函数的定义
专题:
分析:设D的坐标为(-1,-1),连接AD、BD,根据勾股定理的逆定理求得△ABD是直角三角形,从而求得BD∥AC,得出∠ABD=∠BAC,解直角三角形即可求得.
解答: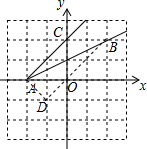 解:如图,设D的坐标为(-1,-1),连接AD、BD,
解:如图,设D的坐标为(-1,-1),连接AD、BD,
∵A(-2,0),C(0,2),
∴∠CAO=45°,∠OAD=45°,
∴∠CAD=90°,
∵AB2=(2+2)2+(2-0)2=20,AD2=(-1+2)2+(0+1)2=2,BD2=(2+1)2+(2+1)2=18,
∴AB2=AD2+BD2,
∴∠ADB=90°,
∴BD∥AC,
∴∠ABD=∠BAC,
∵AD=
,BD=3
,
∴tan∠BAC=tan∠ABD=
=
=
.
故答案为
.
 解:如图,设D的坐标为(-1,-1),连接AD、BD,
解:如图,设D的坐标为(-1,-1),连接AD、BD,∵A(-2,0),C(0,2),
∴∠CAO=45°,∠OAD=45°,
∴∠CAD=90°,
∵AB2=(2+2)2+(2-0)2=20,AD2=(-1+2)2+(0+1)2=2,BD2=(2+1)2+(2+1)2=18,
∴AB2=AD2+BD2,
∴∠ADB=90°,
∴BD∥AC,
∴∠ABD=∠BAC,
∵AD=
| 2 |
| 2 |
∴tan∠BAC=tan∠ABD=
| AD |
| BD |
| ||
3
|
| 1 |
| 3 |
故答案为
| 1 |
| 3 |
点评:此题主要考查了勾股定理,勾股定理逆定理,以及锐角三角函数定义,关键是证明BD∥AC.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列四个命题:①三个角都相等的三角形是等边三角形;②有两个角等于60°的三角形是等边三角形;③有一个角时60°的等腰三角形是等边三角形;④两个角相等的等腰三角形是等边三角形,其中,假命题有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
已知函数y=(m2+m)x2+mx+4为二次函数,则m的取值范围是( )
| A、m≠0 |
| B、m≠-1 |
| C、m≠0,且m≠-1 |
| D、m=-1 |
在平面直角坐标系中,我们把横坐标和纵坐标都是整数的点称为格点,则到坐标原点O的距离为10的格点共有( )个.
| A、4 | B、6 | C、8 | D、12 |
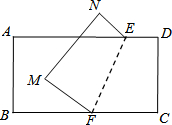 如图,将一张长方形的纸片沿折痕E、F翻折,使点C、D分别落在点M、N的位置,且∠BFM=
如图,将一张长方形的纸片沿折痕E、F翻折,使点C、D分别落在点M、N的位置,且∠BFM=| 1 |
| 2 |
| A、30° | B、36° |
| C、45° | D、60° |
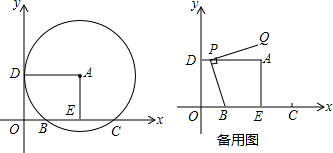
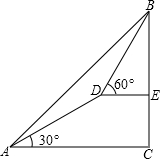 某测量对在山脚A处测得山上树顶仰角为45°(如图),测量队在上坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,求山高为多少米?(精确到1米,
某测量对在山脚A处测得山上树顶仰角为45°(如图),测量队在上坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,求山高为多少米?(精确到1米,