题目内容
某校500名学生参加一次测试,测试分数均大于或等于60且小于100,分数段的频率分布情况如表所示(其中每个分数段可包括最小值,不包括最大值),测试分数在70~80分数段的学生有 名.
| 分数段 | 60~70 | 70~80 | 80~90 | 90~100 |
| 频率 | 0.25 | 0.25 | 0.2 |
考点:频数(率)分布表
专题:
分析:利用总数500乘以对应的频率即可求解.
解答:解:测试分数在70~80分数段的学生是:500×(1-0.25-0.25-0.2)=150(名).
故答案是:150.
故答案是:150.
点评:本题用到的知识点是:频数分布表,理解频率=频数÷总数是解决本题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
已知函数y=(m2+m)x2+mx+4为二次函数,则m的取值范围是( )
| A、m≠0 |
| B、m≠-1 |
| C、m≠0,且m≠-1 |
| D、m=-1 |
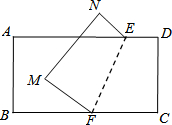 如图,将一张长方形的纸片沿折痕E、F翻折,使点C、D分别落在点M、N的位置,且∠BFM=
如图,将一张长方形的纸片沿折痕E、F翻折,使点C、D分别落在点M、N的位置,且∠BFM=| 1 |
| 2 |
| A、30° | B、36° |
| C、45° | D、60° |
在Rt△ABC中,若各边的长度同时都扩大b倍,则锐角A的正弦值与余弦值的情况( )
| A、都扩大n倍 |
| B、都缩小n倍 |
| C、都不变 |
| D、正弦值扩大n倍,余弦值缩小n倍 |
 如图是两个可以自由转动的转盘,每个转盘被分成两个扇形,同时转动两个转盘,转盘停止后,指针所指区域内的数字之和为偶数的概率是( )
如图是两个可以自由转动的转盘,每个转盘被分成两个扇形,同时转动两个转盘,转盘停止后,指针所指区域内的数字之和为偶数的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知线段AB=12cm,点C是AB的中点,点D在直线AB上,且AB=3BD.求线段CD的长.
如图,已知线段AB=12cm,点C是AB的中点,点D在直线AB上,且AB=3BD.求线段CD的长.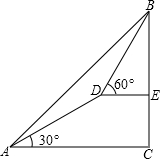 某测量对在山脚A处测得山上树顶仰角为45°(如图),测量队在上坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,求山高为多少米?(精确到1米,
某测量对在山脚A处测得山上树顶仰角为45°(如图),测量队在上坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,求山高为多少米?(精确到1米,