题目内容
19.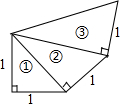 如图所示,一直按此规律进行下去,试求第10个直角三角形的斜边长为多少?第n个直角三角形的斜边长又为多少?
如图所示,一直按此规律进行下去,试求第10个直角三角形的斜边长为多少?第n个直角三角形的斜边长又为多少?
分析 先求出第一个直角三角形的斜边长,再求出第二、三个斜边长,找出规律即可得出结论.
解答 解:解:∵在第一个直角三角形中,斜边长=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$;
在第二个直角三角形中,斜边长=$\sqrt{{1}^{2}+(\sqrt{2})^{2}}$=$\sqrt{3}$;
在第三个直角三角形中,斜边长=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=$\sqrt{4}$,
…,
∴第10个直角三角形斜边长=$\sqrt{{1}^{2}+(\sqrt{10})^{2}}$=$\sqrt{11}$,
第n个直角三角形的斜边长=$\sqrt{{1}^{2}+(\sqrt{n})^{2}}$=$\sqrt{1+n}$.
第10个直角三角形的斜边长为$\sqrt{11}$,第n个直角三角形的斜边长为$\sqrt{n+1}$.
点评 本题考查的是勾股定理,根据题意找出规律是解答此题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
11.如果三角形的一个外角的平分线平行于三角形的一边,那么这个三角形是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
9.2016年,王先生到银行存了一笔三年期的定期存款,年利率是2.75%,若到期后取出,得到本息和 (本金+利息) 为33852元.若设王先生存入的本金为x元,则下面所列方程正确的是( )
| A. | x+3×2.75%x=33825 | B. | x+2.75%+=33825 | ||
| C. | 3×2.75%x=33825 | D. | 3(x+2.75%x)=33825 |
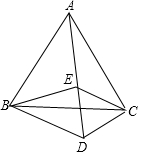 如图,△ABC和△CDE都是等边三角形,点A、E、D在同一条直线上,且∠EBD=62°,求∠AEB的度数.
如图,△ABC和△CDE都是等边三角形,点A、E、D在同一条直线上,且∠EBD=62°,求∠AEB的度数.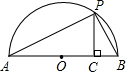 已知a、b是正实数,那么,$\frac{a+b}{2}$$≥\sqrt{ab}$是恒成立的.
已知a、b是正实数,那么,$\frac{a+b}{2}$$≥\sqrt{ab}$是恒成立的.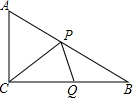 如图,Rt△ABC中,∠ACB=90°,CA=3cm,CB=4cm,设点P、Q为AB、CB上动点,它们分别从A、C同时出发向B点匀速移动,移动速度都为1cm/秒,移动时间为t秒(0≤t≤4),在整个移动过程中,
如图,Rt△ABC中,∠ACB=90°,CA=3cm,CB=4cm,设点P、Q为AB、CB上动点,它们分别从A、C同时出发向B点匀速移动,移动速度都为1cm/秒,移动时间为t秒(0≤t≤4),在整个移动过程中,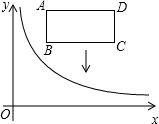 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$ (x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$ (x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).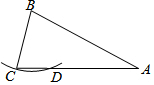 如图,在△ABC中,AB=AC=2BC,以点B为圆心,BC长为半径作弧,与AC交于点D.若AC=4,则线段CD的长为1.
如图,在△ABC中,AB=AC=2BC,以点B为圆心,BC长为半径作弧,与AC交于点D.若AC=4,则线段CD的长为1.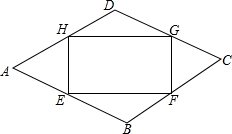 如图,点E、F、G、H分别在菱形ABCD的四条边上,且BE=BF=DG=DH,连接EF,FG,GH,HE得到四边形EFGH,∠A=60°.设AE=x,四边形EFGH的面积为s与边AE的关系为s=-$\sqrt{3}{x}^{2}$+4$\sqrt{3}$x,则菱形边长为4.
如图,点E、F、G、H分别在菱形ABCD的四条边上,且BE=BF=DG=DH,连接EF,FG,GH,HE得到四边形EFGH,∠A=60°.设AE=x,四边形EFGH的面积为s与边AE的关系为s=-$\sqrt{3}{x}^{2}$+4$\sqrt{3}$x,则菱形边长为4.