题目内容
17. 如图,平面直角坐标系中,已知A(0,2),B(2,2),C(1,1).
如图,平面直角坐标系中,已知A(0,2),B(2,2),C(1,1).(1)将△ABC先向左平移2个单位长度,再向下平移1个单位长度,得到△A1B1C1,请画出△A1B1C1,点C1的坐标为(-1,0);
(2)将△ABC绕点O按顺时针方向旋转180°后得到△A2B2C2,点C2的坐标为(-1,-1);
(3)若将△ABC绕点P按顺时针方向旋转90°后得到△A3B3C3,则点P的坐标是(-2,0).
分析 (1)直接利用平移的性质得出对应点位置进而得出答案;
(2)直接利用旋转的性质得出对应点位置进而得出答案;
(3)利用旋转的性质得出旋转中心进而得出等式.
解答  解:(1)如图所示:△A1B1C1,即为所求,点C1的坐标为:(-1,0);
解:(1)如图所示:△A1B1C1,即为所求,点C1的坐标为:(-1,0);
故答案为:(-1,0);
(2)如图所示:△A2B2C2,即为所求,点C2的坐标为(-1,-1);
故答案为:(-1,-1);
(3)如图所示:点P的坐标是(-2,0).
故答案为:(-2,0).
点评 此题主要考查了旋转变换以及平移变换,正确应用旋转的性质是解题关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
8. 如图:AB∥CD,直线MN与AB交于E,过点E作直线HE⊥MN,∠1=130°,则∠2等于( )
如图:AB∥CD,直线MN与AB交于E,过点E作直线HE⊥MN,∠1=130°,则∠2等于( )
 如图:AB∥CD,直线MN与AB交于E,过点E作直线HE⊥MN,∠1=130°,则∠2等于( )
如图:AB∥CD,直线MN与AB交于E,过点E作直线HE⊥MN,∠1=130°,则∠2等于( )| A. | 50° | B. | 40° | C. | 30° | D. | 60° |
6.解方程$\frac{x-2}{x}$-$\frac{3x}{x-2}$=2时,如果设$\frac{x}{x-2}$=y,则原方程可化为关于y的整式方程是( )
| A. | 3y2+2y+1=0 | B. | 3y2+2y-1=0 | C. | 3y2+y+2=0 | D. | 3y2+y-2=0 |
7.若关于x,y的二元一次方程组$\left\{\begin{array}{l}{ax-y=4}\\{x-3y=3}\end{array}\right.$无解,则a的值为( )
| A. | $\frac{1}{3}$ | B. | 1 | C. | -1 | D. | 3 |
 如图,已知A(-2,2),B(-3,-2),C(3,-2)把△ABC向上平移4个单位长度,再向右平移2个单位得到△A1B1C1,解答下列各题:
如图,已知A(-2,2),B(-3,-2),C(3,-2)把△ABC向上平移4个单位长度,再向右平移2个单位得到△A1B1C1,解答下列各题: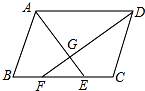 如图,在?ABCD中,∠BAD、∠ADC的平分线AE、DF分别交BC于点E、F,AE与DF相交于点G.
如图,在?ABCD中,∠BAD、∠ADC的平分线AE、DF分别交BC于点E、F,AE与DF相交于点G.