题目内容
若矩形两对角线的夹角为60°,且对角线长为4,则该矩形的长是 .
考点:矩形的性质
专题:
分析:作出图形,根据矩形的对角线互相平分且相等求出OA=OB,然后求出△AOB是等边三角形,根据等边三角形的性质求出AB,再利用勾股定理列式计算即可得解.
解答: 解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴OA=OB=
×4=2,
∵两对角线的夹角∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=2,
在Rt△ABC中,矩形的长BC=
=
=2
.
故答案为:2
.
 解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,∴OA=OB=
| 1 |
| 2 |
∵两对角线的夹角∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=2,
在Rt△ABC中,矩形的长BC=
| AC2-AB2 |
| 42-22 |
| 3 |
故答案为:2
| 3 |
点评:本题考查了矩形的性质,等边三角形的判定与性质,勾股定理,熟记性质是解题的关键,作出图形更形象直观.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
直角三角形两锐角的平分线所夹的钝角的度数为( )
| A、100度 | B、120度 |
| C、135度 | D、140度 |
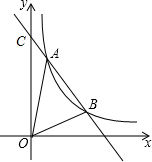 如图,在直角坐标系xOy中,一次函数y=k1x+b的图象与反比例函数y=
如图,在直角坐标系xOy中,一次函数y=k1x+b的图象与反比例函数y= 如图,?ABCD中,DE平分∠ADC交边BC于点E,AD=9,AB=6,则BE=
如图,?ABCD中,DE平分∠ADC交边BC于点E,AD=9,AB=6,则BE= 如图,已知AOB是一条直线,∠1=∠2,∠3=∠4,OF⊥AB.则∠AOC的补角是
如图,已知AOB是一条直线,∠1=∠2,∠3=∠4,OF⊥AB.则∠AOC的补角是