题目内容
 如图,已知AOB是一条直线,∠1=∠2,∠3=∠4,OF⊥AB.则∠AOC的补角是
如图,已知AOB是一条直线,∠1=∠2,∠3=∠4,OF⊥AB.则∠AOC的补角是考点:余角和补角
专题:
分析:(1)根据互为补角的概念:和为180度的两个角互为补角,即可回答.
(2)、(3)根据互为余角的概念:和为90度的两个角互为余角,即可回答.
(4)根据已知,知∠3=∠4,再根据互为补角的概念即可回答.
(2)、(3)根据互为余角的概念:和为90度的两个角互为余角,即可回答.
(4)根据已知,知∠3=∠4,再根据互为补角的概念即可回答.
解答:解:根据题意和图示可知:
(1)∠AOC+∠BOC=180°,则∠AOC的补角是∠COB;
(2)∠AOC+∠3=90°,∠3是∠AOC的余角;
(3)∵∠1=∠2,∠3=∠4,OF⊥AB,
∴∠DOC+∠1+∠3=∠DOC+∠DOF=90°,∠DOC的余角是∠DOF;
(4)∵∠COF+∠1+∠2+∠EOF+∠4=180°,
∴∠COF+∠AOE=180°,∠COF的补角是∠AOE.
故答案为:∠COB;∠3;∠DOF;∠AOE.
(1)∠AOC+∠BOC=180°,则∠AOC的补角是∠COB;
(2)∠AOC+∠3=90°,∠3是∠AOC的余角;
(3)∵∠1=∠2,∠3=∠4,OF⊥AB,
∴∠DOC+∠1+∠3=∠DOC+∠DOF=90°,∠DOC的余角是∠DOF;
(4)∵∠COF+∠1+∠2+∠EOF+∠4=180°,
∴∠COF+∠AOE=180°,∠COF的补角是∠AOE.
故答案为:∠COB;∠3;∠DOF;∠AOE.
点评:主要考查了余角和补角的概念以及运用.互为余角的两角的和为90°,互为补角的两角之和为180度.解此题的关键是能准确的从图中找出角之间的数量关系,从而计算出结果,判断角与角之间的关系.

练习册系列答案
相关题目
若二次根式
有意义,则x的取值范围是( )
| ||
| x-1 |
A、x≥-
| ||
| B、x≠1 | ||
| C、x>1 | ||
D、x≥-
|
方程组
的解为
,则a、b分别为( )
|
|
| A、a=8,b=-2 |
| B、a=8,b=2 |
| C、a=12,b=2 |
| D、a=18,b=8 |
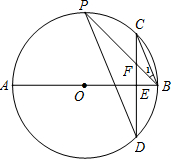 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C. 如图:已知∠B=60°,∠C=20°,∠1=120°,则∠A=
如图:已知∠B=60°,∠C=20°,∠1=120°,则∠A= 某记者抽样调查了某校一些学生假期用于读书的时间(单位:分钟)后,绘制了频数分布直方图,从左到右的前5个长方形相对应的频率之和为0.9,最后一组的频数是15,则此次抽样调查的人数为
某记者抽样调查了某校一些学生假期用于读书的时间(单位:分钟)后,绘制了频数分布直方图,从左到右的前5个长方形相对应的频率之和为0.9,最后一组的频数是15,则此次抽样调查的人数为