题目内容
12.如图,矩形ABCD中,AB=3,AD=4,E为对角线AC上的一个动点,连结DE,EF⊥DE交射线BC与点F,设AE为x.(1)当x取何值时,DE的值最小;
(2)设CF=y,当点F在线段BC上时,求y与x之间的函数关系式;
(3)试探索:当x为何值时,△EFC为等腰三角形?
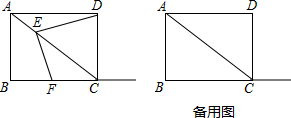
分析 (1)当DE⊥AC时,DE的值最小,利用矩形的性质可证明△AED∽△ADC,利用相似三角形的性质可求得AE的长,即可求得x的值;
(2)过点E作MN⊥BC,分别交AD、BC于M、N,可证明△AME∽△ADC,可用x表示出MD和ME,进一步可证明△DME∽△ENF,可找到y与x之间的关系式;
(3)分点F在线段BC上和在线段BC的延长线上,当点F在线段BC上时,可证明△DEF≌△DCF,可得到DF⊥AC,可求得HC,则可求得AE;当点F 在线段BC的延长线上时,可证明AD=AE,可求得AE的长,则可得出x的值.
解答 解:
(1)当DE⊥AC时,DE的值最小,
∵四边形ABCD是矩形,
∴∠ADC=90°,且AD=4,AB=3,
∴AC=5,
∵DE⊥AC,
∴△ADE∽△ACD,
∴$\frac{AD}{AC}$=$\frac{AE}{AD}$,即$\frac{4}{5}$=$\frac{AE}{4}$,解得AE=$\frac{16}{5}$,
∴x的值为$\frac{16}{5}$;
(2)如图1,过点E作MN⊥BC,分别交AD、BC于M、N,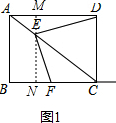
∵MN∥DC,
∴△AME∽△ADC,
∴$\frac{AM}{AD}$=$\frac{ME}{CD}$=$\frac{AE}{AC}$,即$\frac{AM}{4}$=$\frac{ME}{3}$=$\frac{x}{5}$,
∴AM=$\frac{4}{5}$x,ME=$\frac{3}{5}$x,
∴MD=4-$\frac{4}{5}$x,NE=3-$\frac{3}{5}$x,
∵∠DEF=90°,
∴∠DEM+∠FEN=90°,
∵∠DME=90°,
∴∠DEM+∠EDM=90°,
∴∠EFN=∠EDM,
∵∠DME=∠ENF=90°,
∴△DME∽△ENF,
∴$\frac{DM}{EN}$=$\frac{ME}{NF}$,即$\frac{4-\frac{4}{5}x}{3-\frac{3}{5}x}$=$\frac{\frac{3}{5}x}{NF}$,
∴NF=$\frac{9}{20}$x,
∵CF=BC-FN-NF,
∴y=4-$\frac{4}{5}$x-$\frac{9}{20}$x=4-$\frac{5}{4}$x;
(3)当点F在线段BC上时,如图2,连接DF,交AC于点H,
∵∠EFC>90°,
∴当△EFC为等腰三角形时,则有FE=FC,
在R△DEF和Rt△DCF中
$\left\{\begin{array}{l}{EF=CF}\\{DF=DF}\end{array}\right.$
∴△DEF≌△DCF(HL),
∴∠EFD=∠CFD,
∴DF⊥AC,
由(1)可知AH=$\frac{16}{5}$,
∴HC=AC-AH=5-$\frac{16}{5}$=$\frac{9}{5}$,
∴AE=5-2HC=5-$\frac{9}{5}$×2=$\frac{7}{5}$;
当点F在BC的延长线上时,如图3,延长DE交BC于H,
∵∠ECF>90°,
∴当△EFC为等腰三角形时,则有CE=CF,
∵∠FEH=90°,CE=CF,
∴∠F=∠CEF,
∴∠F+∠EHC=∠HEC+∠CEF=90°,
∴∠EHC=∠HEC,
∵AD∥BC,
∴∠ADE=∠CHE,∠AED=∠CEH,
∴∠ADE=∠AED,
∴AE=AD=4;
综上可知当△EFC为等腰三角形时,x的值为$\frac{7}{5}$或4.
点评 本题为四边形的综合应用,涉及知识点有矩形的性质、相似三角形的判定和性质、全等三角形的判定和性质、等腰三角形的性质及分类讨论思想.在(1)中确定出DE最小值时E点的位置是解题的关键,在(2)中用x表示出NF是解题的关键,在(3)中注意分两种情况.本题考查知识点较多,综合性较强,难度适中.

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案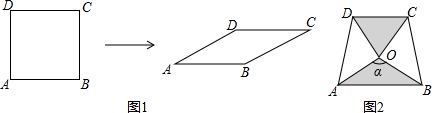
(1)请补全表:
| α | 30° | 45° | 60° | 90° | 120° | 135° | 150° |
| S | $\frac{1}{2}$ | 1 | $\frac{{\sqrt{2}}}{2}$ |
由(1)可以发现单位正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把单位菱形的面积S记为S(α).例如:当α=30°时,S=S(30°)=$\frac{1}{2}$;当α=135°时,S=S(135°)=$\frac{{\sqrt{2}}}{2}$.由上表可以得到S(60°)=S(120°);S(150°)=S(30°),…,由此可以归纳出S(180°-α)=(α°).
(3)两块相同的等腰直角三角板按图2的方式放置,AD=$\sqrt{2}$,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
| A. | 3-5=2 | B. | 3a+2b=5ab | C. | 4-|-3|=1 | D. | 3x2y-2xy2=xy |
(1)有同学提议:“八年级1班的人数刚好是40人,不如我们直接调查1班所有同学吧”,他的建议合理吗?请说明理由;
(2)他们用问卷随机调查了40位同学(每人只能选一项),并统计如下:
| 第一印象 | 满怀期待 | 忧喜交加 | 想想都累 | 放过我吧 | 其他 |
| 划记 |  | 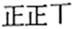 |  | 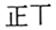 | 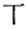 |
(3)若本校八年级共有500名学生,请估计对初三第一印象是“忧喜交加”的同学人数.
 已知实数a,b在数轴上的对应点如图所示,那么化简$\sqrt{(a-b)^{2}}$-$\sqrt{{a}^{2}}$=b.
已知实数a,b在数轴上的对应点如图所示,那么化简$\sqrt{(a-b)^{2}}$-$\sqrt{{a}^{2}}$=b. 如图随意抛掷一枚石子,落在阴影部分的概率是$\frac{1}{4}$.
如图随意抛掷一枚石子,落在阴影部分的概率是$\frac{1}{4}$.