题目内容
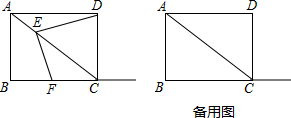
3．
已知实数a，b在数轴上的对应点如图所示，那么化简$\sqrt{（a-b）^{2}}$-$\sqrt{{a}^{2}}$=b．
分析 根据数轴确定a、b的符号以及a、b的大小，根据二次根式的性质化简即可．
解答 解：由数轴可知，a＜0＜b，
则a-b＜0，
∴$\sqrt{（a-b）^{2}}$-$\sqrt{{a}^{2}}$=b-a+a=b，
故答案为：b．
点评 本题考查的是二次根式的化简、数轴的性质，掌握二次根式的性质：$\sqrt{{a}^{2}}$=|a|是解题的关键．
练习册系列答案
相关题目
14．
如图，甲、乙两户居民家庭全年支出费用的扇形统计图，根据统计图，下面对全年食品支出费用判断正确的是（ ）
如图，甲、乙两户居民家庭全年支出费用的扇形统计图，根据统计图，下面对全年食品支出费用判断正确的是（ ）| A． | 甲户比乙户多 | B． | 乙户比甲户多 | ||
| C． | 甲、乙两户一样多 | D． | 无法确定哪一户多 |
11．下列计算正确的是（ ）
| A． | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | B． | $\sqrt{3}•\sqrt{2}$=$\sqrt{6}$ | C． | （$\sqrt{3}$）2=9 | D． | $\sqrt{（-5）^{2}}$=-5 |
15．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
| A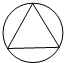． |  | B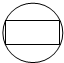． |  | C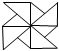． |  | D． |  |
