题目内容
(1)计算:|-2|-
+(-1)2014-
.
(2)解方程组:
.
(3)
.
| 9 |
| 3 | 8 |
(2)解方程组:
|
(3)
|
考点:解二元一次方程组,实数的运算
专题:计算题
分析:(1)原式第一项利用绝对值的代数意义化简,第二项利用平方根定义化简,第三项利用-1的偶次幂计算,最后一项利用立方根的定义化简,计算即可得到结果;
(2)利用加减消元法求出方程组的解即可;
(3)方程组变形后,利用加减消元法求出解即可.
(2)利用加减消元法求出方程组的解即可;
(3)方程组变形后,利用加减消元法求出解即可.
解答:解:(1)原式=2-3+1-(-2)
=2;
(2)
,
①+②得:x=-1,
把x=-1代入①得:y=2,
∴原方程组的解为
;
(3)
,
①×3-②×2得:x=-1,
将x=-1代入①得:y=2,
则方程组的解为
.
=2;
(2)
|
①+②得:x=-1,
把x=-1代入①得:y=2,
∴原方程组的解为
|
(3)
|
①×3-②×2得:x=-1,
将x=-1代入①得:y=2,
则方程组的解为
|
点评:此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目

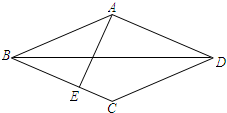 已知:如图,在菱形ABCD中,AE⊥BC,垂足为E,对角线BD=4,tan∠CBD=
已知:如图,在菱形ABCD中,AE⊥BC,垂足为E,对角线BD=4,tan∠CBD=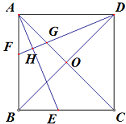 如图所示,四边形ABCD是正方形,AC、BD交于点O,AE平分∠BAC,DF垂直AE,交AB于点F,交AE于点H,交AC于点G.求证:
如图所示,四边形ABCD是正方形,AC、BD交于点O,AE平分∠BAC,DF垂直AE,交AB于点F,交AE于点H,交AC于点G.求证: 如图,ED∥FB,且∠1+∠2=180°.求证:∠AGF=∠ABC.
如图,ED∥FB,且∠1+∠2=180°.求证:∠AGF=∠ABC. 如图,⊙O的直径为5,在⊙O上位于直径AB的异侧有定点C和动点P,已知
如图,⊙O的直径为5,在⊙O上位于直径AB的异侧有定点C和动点P,已知