题目内容
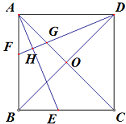 如图所示,四边形ABCD是正方形,AC、BD交于点O,AE平分∠BAC,DF垂直AE,交AB于点F,交AE于点H,交AC于点G.求证:
如图所示,四边形ABCD是正方形,AC、BD交于点O,AE平分∠BAC,DF垂直AE,交AB于点F,交AE于点H,交AC于点G.求证:(1)OG=
| 1 |
| 2 |
(2)AE=DF.
考点:正方形的性质
专题:证明题
分析:(1)过点B作BP⊥BD交DF的延长线与点P,利用三角形的中位线,得出OG=
PB,再利用AE平分∠BAC,DF⊥AE,对顶角相等,以及三角形的内角和,求得∠P=∠PFB,得出PB=BF得出最后结论;

(2)由正方形的性质证得△ABE≌△DAF,得出结论即可.
| 1 |
| 2 |

(2)由正方形的性质证得△ABE≌△DAF,得出结论即可.
解答:解:(1)如图,

过点B作BP⊥BD交DF的延长线与点P,
∵四边形ABCD是正方形,
∴AC⊥BD,OB=OD
∴PB∥AC,
∴DG=PG
∴OG=
PB
∵AE平分∠BAC,∠BAC=45,DF⊥AE
∴∠HAG=∠HAF=∠GDO=22.5°
∴∠AFH=∠AGH=∠P=67.5°
∴∠PFB=∠AFH=∠P=67.5°
∴PB=BF
∴OG=
BF.
(2)∵∠AEB=90°-∠EAB=67.5°,
∴∠AFD=∠AEB,
在△ABE和△DAF中,
∴△ABE≌△DAF(AAS),
∴AE=DF.

过点B作BP⊥BD交DF的延长线与点P,
∵四边形ABCD是正方形,
∴AC⊥BD,OB=OD
∴PB∥AC,
∴DG=PG
∴OG=
| 1 |
| 2 |
∵AE平分∠BAC,∠BAC=45,DF⊥AE
∴∠HAG=∠HAF=∠GDO=22.5°
∴∠AFH=∠AGH=∠P=67.5°
∴∠PFB=∠AFH=∠P=67.5°
∴PB=BF
∴OG=
| 1 |
| 2 |
(2)∵∠AEB=90°-∠EAB=67.5°,
∴∠AFD=∠AEB,
在△ABE和△DAF中,
|
∴△ABE≌△DAF(AAS),
∴AE=DF.
点评:此题考查正方形的性质,三角形全等的判定与性质,以及等腰三角形的判定与性质,注意利用正方形中的特殊角度是解决问题的关键.

练习册系列答案
相关题目
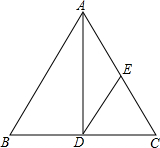 如图,AD是等腰三角形ABC的底边BC上的高,DE∥AB,交AC于点E,试找出图中的一个等腰三角形(△ABC除外),并说明理由.我找的等腰三角形是
如图,AD是等腰三角形ABC的底边BC上的高,DE∥AB,交AC于点E,试找出图中的一个等腰三角形(△ABC除外),并说明理由.我找的等腰三角形是 如图,AB是直径,CA切⊙O于点A,连接BC交⊙O点D,E是弧BD的中点,连接AE交BC于点F.
如图,AB是直径,CA切⊙O于点A,连接BC交⊙O点D,E是弧BD的中点,连接AE交BC于点F.
 如图,在?ABCD中,点E、F分别在边AB、CD上.
如图,在?ABCD中,点E、F分别在边AB、CD上.