题目内容
(1)化简:
+
.
(2)先化简,再求值:(
-4)÷
,其中x=-1.
| a-3b |
| a-b |
| a+b |
| a-b |
(2)先化简,再求值:(
| x2+4 |
| x |
| x2-4 |
| x2+2x |
考点:分式的化简求值
专题:
分析:(1)根据分式分母相同,直接计算进而化简求出即可;
(2)首先将括号里面通分,进而将能因式分解的分子与分母因式分解,即可化简,再利用分式有意的条件得出即可.
(2)首先将括号里面通分,进而将能因式分解的分子与分母因式分解,即可化简,再利用分式有意的条件得出即可.
解答:解:(1)原式=
=
=
=2;
(2)(
-4)÷
=
÷
=
•
=x-2.
当x=-1时,原式=-1-2=-3.
| a-3b+a+b |
| a-b |
| 2a-2b |
| a-b |
| 2(a-b) |
| a-b |
(2)(
| x2+4 |
| x |
| x2-4 |
| x2+2x |
=
| x2+4-4x |
| x |
| (x+2)(x-2) |
| x(x+2) |
=
| (x-2)2 |
| x |
| x(x+2) |
| (x+2)(x-2) |
当x=-1时,原式=-1-2=-3.
点评:此题主要考查了分式的化简求值,在分式运算的过程中,要注意对分式的分子、分母进行因式分解,然后简化运算,再运用四则运算法则进行求值计算.分式混合运算的顺序是先乘方,后乘除,最后加减,有括号的先算括号内的,其乘除运算归根到底是乘法运算,实质是约分,分式加减实质是通分,结果要化简.关于化简求值,近年来出现了一种开放型问题,题目中给定几个数字,要考虑分母有意义的条件,不要盲目代入.

练习册系列答案
相关题目
下列运算正确的是( )
A、
| ||||||||||
B、
| ||||||||||
C、-4
| ||||||||||
D、
|

 如图,AB是直径,CA切⊙O于点A,连接BC交⊙O点D,E是弧BD的中点,连接AE交BC于点F.
如图,AB是直径,CA切⊙O于点A,连接BC交⊙O点D,E是弧BD的中点,连接AE交BC于点F.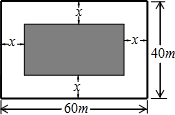 如图,为了给小区居民增加锻炼场所,物业拟在一宽为40米、长为60米的矩形区域内的四周修建宽度相同的鹅卵石小路,阴影部分用作绿化.当阴影部分面积为800平方米时,小路宽x为多少米.
如图,为了给小区居民增加锻炼场所,物业拟在一宽为40米、长为60米的矩形区域内的四周修建宽度相同的鹅卵石小路,阴影部分用作绿化.当阴影部分面积为800平方米时,小路宽x为多少米.