题目内容
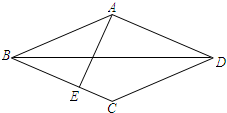 已知:如图,在菱形ABCD中,AE⊥BC,垂足为E,对角线BD=4,tan∠CBD=
已知:如图,在菱形ABCD中,AE⊥BC,垂足为E,对角线BD=4,tan∠CBD=| 1 |
| 2 |
(1)边AB的长;
(2)∠ABE的正弦值.
考点:菱形的性质,解直角三角形
专题:
分析:(1)首先连接AC,AC与BD相交于点O,由四边形ABCD是菱形,可得AC⊥BD,BO=
BD=2,又由tan∠CBD=
,可求得OC的长,然后由勾股定理求得边AB的长;
(2)由AE⊥BC,利用S菱形ABCD=BC•AE=
BD•AC,即可求得AE的长,继而求得∠ABE的正弦值.
| 1 |
| 2 |
| 1 |
| 2 |
(2)由AE⊥BC,利用S菱形ABCD=BC•AE=
| 1 |
| 2 |
解答: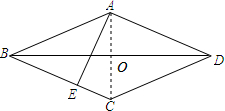 解:(1)连接AC,AC与BD相交于点O,
解:(1)连接AC,AC与BD相交于点O,
∵四边形ABCD是菱形,
∴AC⊥BD,BO=
BD=2,
∵Rt△BOC中,tan∠CBD=
=
,
∴OC=1,
∴AB=BC=
=
;
(2)∵AE⊥BC,
∴S菱形ABCD=BC•AE=
BD•AC,
∵AC=2OC=2,
∴
AE=
×2×4,
∴AE=
,
∴sin∠ABE=
=
.
 解:(1)连接AC,AC与BD相交于点O,
解:(1)连接AC,AC与BD相交于点O,∵四边形ABCD是菱形,
∴AC⊥BD,BO=
| 1 |
| 2 |
∵Rt△BOC中,tan∠CBD=
| OC |
| OB |
| 1 |
| 2 |
∴OC=1,
∴AB=BC=
| BO2+OC2 |
| 5 |
(2)∵AE⊥BC,
∴S菱形ABCD=BC•AE=
| 1 |
| 2 |
∵AC=2OC=2,
∴
| 5 |
| 1 |
| 2 |
∴AE=
4
| ||
| 5 |
∴sin∠ABE=
| AE |
| AB |
| 4 |
| 5 |
点评:此题考查了菱形的性质、勾股定理以及三角函数等知识.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
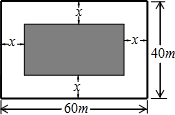 如图,为了给小区居民增加锻炼场所,物业拟在一宽为40米、长为60米的矩形区域内的四周修建宽度相同的鹅卵石小路,阴影部分用作绿化.当阴影部分面积为800平方米时,小路宽x为多少米.
如图,为了给小区居民增加锻炼场所,物业拟在一宽为40米、长为60米的矩形区域内的四周修建宽度相同的鹅卵石小路,阴影部分用作绿化.当阴影部分面积为800平方米时,小路宽x为多少米.