题目内容
 如图,⊙O的直径为5,在⊙O上位于直径AB的异侧有定点C和动点P,已知
如图,⊙O的直径为5,在⊙O上位于直径AB的异侧有定点C和动点P,已知BC:CA=4:3,点P在半圆弧AB上运动(不与A、B两点重合),过点C作CP的垂线CD交PB的延长线于D点.
(1)当点P在弧AB上运动到何处时,CD与⊙O相切.(直接说出结论,不用说理)
(2)连接AP,求证:△PCA∽△DCB;
(3)当点P运动到AB弧中点时,求CD的长.
考点:切线的判定,相似三角形的判定与性质
专题:
分析:(1)根据切线的判定方法,当PC为⊙O的直径时即可符合题意;
(2)利用圆周角定理得出∠ACB=90°,进而得出∠ABC=∠APC,再利用相似三角形的判定得出即可;
(3)首先求出AC,PA,PB长,进而利用勾股定理得出MC和PM的长,进而得出DC的长.
(2)利用圆周角定理得出∠ACB=90°,进而得出∠ABC=∠APC,再利用相似三角形的判定得出即可;
(3)首先求出AC,PA,PB长,进而利用勾股定理得出MC和PM的长,进而得出DC的长.
解答:解:(1)当PC经过圆心O时,CD与⊙O相切.
(2)如图1,由题意,AB是⊙O的直径;∴∠ACB=90°,
∵CD⊥CP,∴∠PCD=90°
∴∠ACP+∠BCP=∠PCB+∠DCB=90°,
∴∠ACP=∠DCB,
又∵∠CBP=∠D+∠DCB,∠CBP=∠ABP+∠ABC,
∴∠ABC=∠APC,
∴∠APC=∠D,
∴△PCA∽△DCB;
(3)如图2,当P运动到AB弧的中点时,连接AP,过A作AM⊥CP,垂足为M,
∵AB是⊙O的直径,
∴∠APB=90°,
又∵P是弧AB的中点,
∴
=
,
∴AP=BP,
∴∠PAB=∠PBA=45°,
又AB=5,
∴PA=PB=
,
在Rt△ABC中,
∵BC:CA=4:3,AB=5,
∴AC=3,
在Rt△AMC中,∠ACM=45°,
∴∠CAM=45,∴AM=CM=
,
在Rt△AMP中,AP2+AM2=PM2,
∴PM=2
,
∴PC=PM+
=
.
由(2)△PCA∽△DCB知:AC•CD=PC•BC,
3×CD=PC×4,
∴CD=
.
(2)如图1,由题意,AB是⊙O的直径;∴∠ACB=90°,
∵CD⊥CP,∴∠PCD=90°
∴∠ACP+∠BCP=∠PCB+∠DCB=90°,
∴∠ACP=∠DCB,
又∵∠CBP=∠D+∠DCB,∠CBP=∠ABP+∠ABC,
∴∠ABC=∠APC,
∴∠APC=∠D,
∴△PCA∽△DCB;
(3)如图2,当P运动到AB弧的中点时,连接AP,过A作AM⊥CP,垂足为M,
∵AB是⊙O的直径,
∴∠APB=90°,
又∵P是弧AB的中点,

∴
 |
| AP |
 |
| PB |
∴AP=BP,
∴∠PAB=∠PBA=45°,
又AB=5,
∴PA=PB=
5
| ||
| 2 |
在Rt△ABC中,
∵BC:CA=4:3,AB=5,
∴AC=3,
在Rt△AMC中,∠ACM=45°,
∴∠CAM=45,∴AM=CM=
3
| ||
| 2 |
在Rt△AMP中,AP2+AM2=PM2,
∴PM=2
| 2 |
∴PC=PM+
3
| ||
| 2 |
7
| ||
| 2 |
由(2)△PCA∽△DCB知:AC•CD=PC•BC,
3×CD=PC×4,
∴CD=
14
| ||
| 3 |
点评:此题主要考查了切线的判定以及相似三角形的判定与性质和勾股定理等知识,熟练利用勾股定理得出PM的长是解题关键.

练习册系列答案
相关题目


 如图,在?ABCD中,点E、F分别在边AB、CD上.
如图,在?ABCD中,点E、F分别在边AB、CD上.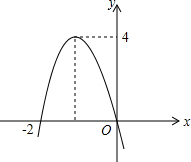 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+k=0有实数解,则k的最小值为
二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+k=0有实数解,则k的最小值为